题目内容
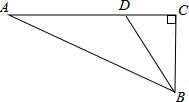如图，在△ABC中，∠C=90°，BD平分∠ABC，交AC于点D，AC=14cm，且CD：AD=2：5，则点D到AB的距离为考点：角平分线的性质
专题：
分析：过点D作DE⊥AB于E，根据角平分线上的点到角的两边距离相等可得DE=CD，再根据比例求出CD即可得解．
解答：
解：如图，过点D作DE⊥AB于E，
∵∠C=90°，BD平分∠ABC，
∴DE=CD，
∵AC=14cm，CD：AD=2：5，
∴CD=
×14=4cm，
∴DE=4cm，
即点D到AB的距离为4cm．
故答案为：4．
解：如图，过点D作DE⊥AB于E，∵∠C=90°，BD平分∠ABC，
∴DE=CD，
∵AC=14cm，CD：AD=2：5，
∴CD=
| 2 |
| 2+5 |
∴DE=4cm，
即点D到AB的距离为4cm．
故答案为：4．
点评：本题考查了角平分线上的点到角的两边距离相等的性质，熟记性质是解题的关键．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
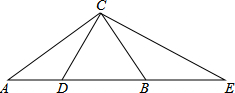如图，在Rt△ABC中，∠ACB=90°，AC=b，AB=c．若D、E分别是AB和AB延长线上的两点，BD=BC，CE⊥CD，则以AD和AE的长为根的一元二次方程是（ ）| A、x2-2cx+b2=0 |
| B、x2-cx+b2=0 |
| C、x2-2cx+b=0 |
| D、x2-cx+b=0 |
若a的相反数是-3，则a的倒数是（ ）
A、-
| ||
| B、-3 | ||
C、
| ||
| D、3 |