题目内容
1.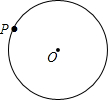 已知:如图,P是⊙0上的一点.
已知:如图,P是⊙0上的一点.(1)在⊙0上求作一点B,使PB是⊙0的内接正三角形的一边;
(2)在$\widehat{BP}$上求作一点A,使PA是⊙0的内接正方形的一边;
(3)连接0B,求∠A0B的度数;
(4)求作⊙0的内接正十二边形.
分析 (1)根据正六边形的特点作出⊙0的内接正三角形的一边;
(2)根据圆内接正四边形的中心角是90°解答即可;
(3)分别计算出正三角形和正四边形的中心角,计算即可;
(4)根据正六边形的特点作图即可.
解答 解:(1)以P为圆心、OP为半径在⊙0上依次截取2个点,第二个点为B,则PB即为所求;
(2)作直径PH,过圆心作直径PH的垂线交$\widehat{BP}$于点A,则PA即为所求;
(3)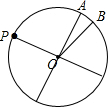 ∵PA是⊙0的内接正方形的一边,
∵PA是⊙0的内接正方形的一边,
∴∠AOP=90°,
∵PB是⊙0的内接正三角形的一边,
∴∠BOP=120°,
∴∠A0B=30°;
(4)以P为圆心、OP为半径在⊙0上依次截取6个点,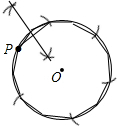
则这6个点是圆的6等分点,
作各弧的中点,顺次连接12个点,得到⊙0的内接正十二边形.
点评 本题考查的是正多边形和圆的知识,提高学生对正多边形的概念掌握和计算的能力是解题的关键.

练习册系列答案
相关题目
9.有一种长方体集装箱,其内空长为5米,高4.5米,宽3.4米,用这样的集装箱运长为5米,横截面的外圆直径为0.8米的圆柱形钢管,最多能运( )根.
| A. | 20根 | B. | 21根 | C. | 24根 | D. | 25根 |
10.用配方法解方程x2+4x-6=0,下列配方正确的是( )
| A. | (x+4)2=22 | B. | (x+2)2=10 | C. | (x+2)2=8 | D. | (x+2)2=6 |
11.下列各题计算正确的是( )
| A. | (ab-1)(-4ab2)=-4a2b3-4ab2 | B. | (3x2+xy-y2)•3x2=9x4+3x3y-y2 | ||
| C. | (-3a)(a2-2a+1)=-3a3+6a2 | D. | (-2x)(3x2-4x-2)=-6x3+8x2+4x |
 已知在△ABC中,AB=BC,D是BC的中点,CF∥AB,试说明BP2=PE•PF.
已知在△ABC中,AB=BC,D是BC的中点,CF∥AB,试说明BP2=PE•PF.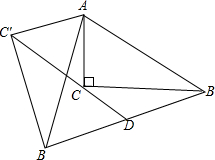 在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转,B、C旋转后的对应点分别是B′和C′.连接C′C并延长交B′B于点D.
在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转,B、C旋转后的对应点分别是B′和C′.连接C′C并延长交B′B于点D.