Question

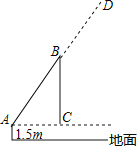
【题目】如图，吊车在水平地面上吊起货物时，吊绳BC与地面保持垂直，吊臂AB与水平线的夹角为64°，吊臂底部A距地面1.5m．（计算结果精确到0.1m，参考数据sin64°≈0.90，cos64°≈0.44，tan64°≈2.05）

（1）当吊臂底部A与货物的水平距离AC为5m时，吊臂AB的长为多少m．

（2）如果该吊车吊臂的最大长度AD为20m，那么从地面上吊起货物的最大高度是多少？（吊钩的长度与货物的高度忽略不计）

Answer 1

【答案】（1）11.4；（2）从地面上吊起货物的最大高度是19.5m．

【解析】

（1）根据直角三角形的性质和三角函数解答即可；

（2）过点D作DH⊥地面于H，利用直角三角形的性质和三角函数解答即可．

（1）在Rt△ABC中，

∵∠BAC=64°，AC=5m，

∴AB= 5÷0.4411.4（m）；

（2）过点D作DH⊥地面于H，交水平线于点E，

在Rt△ADE中，

∵AD=20m，∠DAE=64°，EH=1.5m，

∴DE=sin64°×AD≈20×0.9≈18（m），

即DH=DE+EH=18+1.5=19.5（m），

答：如果该吊车吊臂的最大长度AD为20m，那么从地面上吊起货物的最大高度是19.5m．