Question

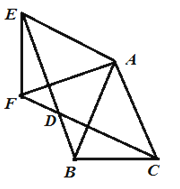
【题目】如图△ABC，AB=AC，将△ABC绕点A顺时针旋转得到△AEF，连结BE、CF相交于点D．

（1）求证：BE=CF；

（2）已知四边形ACDE是菱形，∠BAC=45°，AB=AC=1．

①求旋转角 ∠BAE的度数；

②求BD的长．

Answer 1

【答案】（1）证明见解析；（2）①90°；②

【解析】

（1）先由旋转的性质得AE=AB，AF=AC，∠EAF=∠BAC，则∠EAF+∠BAF=∠BAC+∠BAF，即∠EAB=∠FAC，利用AB=AC可得AE=AF，于是根据旋转的定义，△AEB可由△AFC绕点A按顺时针方向旋转得到，然后根据旋转的性质得到BE=CD；

（2）①由菱形的性质得到DE=AE=AC=AB=1，AC∥DE，根据等腰三角形的性质得∠AEB=∠ABE，根据平行线得性质得∠ABE=∠BAC=45°，所以∠AEB=∠ABE=45°，于是可判断△ABE为等腰直角三角形，即可求出∠BAE的度数；

②由△ABE为等腰直角三角形，可求出BE=AC=再利用BD=BE-DE即可求解．

(1)证明：∵△AEF是由△ABC绕点A按顺时针方向旋转得到的，

∴AE=AB，AF=AC，∠EAF=∠BAC，

∴∠EAF+∠BAF=∠BAC+∠BAF，

即∠EAB=∠FAC，

∵AB=AC，

∴AE=AF，

∴△AEB可由△AFC绕点A按顺时针方向旋转得到，

∴BE=CF；

(2)解：①∵四边形ACDE为菱形，AB=AC=1，

∴DE=AE=AC=AB=1,AC∥DE，

∴∠AEB=∠ABE,∠ABE=∠BAC=45°，

∴∠AEB=∠ABE=45°，

∴△ABE为等腰直角三角形，

∴∠BAE＝90°；

②∵△ABE为等腰直角三角形，

∴BE=AC=，

∴BD=BEDE=1.