题目内容
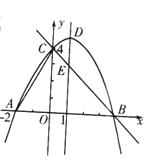
【题目】如图，抛物线
与
轴交于点C(O，4)，与
轴交于点A和点B，其中点A的坐标为（－2,0），抛物线的对称轴
与抛物线交于点D，与直线BC交于点E．
(1)求抛物线的解析式；
(2)若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积为17，若存在，求出点F的坐标；若不存在，请说明理由；
(3)平行于DE的一条动直线Z与直线BC相交于点P，与抛物线相交于点Q，若以D、E、P、Q为顶点的四边形是平行四边形，求点P的坐标。
【答案】（1）抛物线的解析式是
；
（2）不存在满足条件的点F；
（3）满足条件的点P有三个，分别是P1 (3,1)，P2（2+
，2 －），P3（2—，2十）
【解析】
试题（1）先把C（0，4）代入y=ax2+bx+c，得出c=4①，再由抛物线的对称轴x=-
=1，得到b=-2a②，抛物线过点A（-2，0），得到0=4a-2b+c③，然后由①②③可解得，a=-
，b=1，c=4，即可求出抛物线的解析式为y=-x2+x+4；（2）假设存在满足条件的点F，连结BF、CF、OF，过点F作FH⊥x轴于点H，FG⊥y轴于点G．设点F的坐标为（t，-t2+t+4），则FH=-t2+t+4，FG=t，先根据三角形的面积公式求出S△OBF=OBFH=-t2+2t+8，S△OFC=OCFG=2t，再由S四边形ABFC=S△AOC+S△OBF+S△OFC，得到S四边形ABFC=-t2+4t+12．令-t2+4t+12=17，即t2-4t+5=0，由△=（-4）2-4×5=-4<0，得出方程t2-4t+5=0无解，即不存在满足条件的点F；
（3）先运用待定系数法求出直线BC的解析式为y=-x+4，再求出抛物线y=-x2+x+4的顶点D（1，
），由点E在直线BC上，得到点E（1，3），于是DE=-3=
．若以D、E、P、Q为顶点的四边形是平行四边形，因为DE∥PQ，只须DE=PQ，设点P的坐标是（m，-m+4），则点Q的坐标是（m，-m2+m+4）．分两种情况进行讨论：①当0<m<4时，PQ=（-m2+m+4）-（-m+4）=-m2+2m，解方程-m2+2m=，求出m的值，得到P1（3，1）；②当m<0或m>4时，PQ=（-m+4）-（-m2+m+4）=m2-2m，解方程
m2-2m=，求出m的值，得到P2（2+
，2-），P3（2-，2+）．
试题解析：(1)由抛物线经过点C(O，4)可得c=4,①
∵对称轴x=
=1，∴b=－2a，②，
又抛物线过点A（一2，O）∴0=4a－2b+c，③
由①②③ 解得：a=
, b=1 ,c=4．
所以抛物线的解析式是
(2)假设存在满足条件的点F，连接BF、CF、OF．
过点F分别作FH⊥x轴于H , FG⊥y轴于G．
设点F的坐标为（t, 
+t+4），其中O<t<4， 则FH=+t+4 FG=t,
∴
=OB.FH=×4×（+4t+4）=-
+2t+8 ,
=OC.FC=×4×t=2t
令-+4t+12 =17，即－4t+5=0，则△= -4<0,
∴方程
－4t+5=0无解，故不存在满足条件的点F．
(3)设直线BC的解析式为y=kx+b（k≠O），又过点B(4，0)， C(0，4)
所以
，解得：
，
所以直线BC的解析式是y= -x+4．
由y=
+4x+4=
+，得D（1，），
又点E在直线BC上，则点E(1，3)，
于是DE=-3= .
若以D.E.P.Q为顶点的四边形是平行四边形，
因为DE∥PQ，只须DE=PQ,
设点P的坐标是（m，-m+4），则点Q的坐标是（m，-
+m+4）．
①当O<m<4时，PQ=（-+m+4）-（-m+4）= -+2m．
由-+2m= ，解得：m=1或3．
当m=1时，线段PQ与DE重合,m=－1舍去,
∴m=－3，此时P1 (3，1)．
②当m<0或m>4时，PQ=（-m+4）-（-++m+4)= -2m,
由
-2m=，解得m=2±，经检验适合题意，
此时P2（2+，2-），P3（2-，2+）．
综上所述，满足条件的点P有三个，分别是P1 (3，1)，P2（2+，2 －），P3（2-，2+）
