题目内容
16．
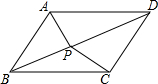如图，P为平行四边形ABCD中一点，△APB、△BPC、△PDC的面积分别为12、13、18．则△APD的面积为17．
分析 由于平行四边形的两组对边分别相等，且S△BPC，S△APD的高的和是AD，BC间的距离，所以得到S△BPC+S△APD=$\frac{1}{2}$S?ABCD，同理可得S△APB+S△PDC=$\frac{1}{2}$S?ABCD，即可求出结果．
解答 解：∵平行四边形的两组对边分别相等，
且S△BPC，S△APD的高的和是AD，BC间的距离，
它们的底分别是AD，BC，而AD=BC，
∴S△BPC+S△APD和平行四边形是等底等高，
∴S△BPC+S△APD=$\frac{1}{2}$S?ABCD，
同理可得S△APB+S△PDC=$\frac{1}{2}$S?ABCD，
∴S△APB+S△PDC=S△BPC+S△APD，
∴12+18=13+S△APD，
∴S△APD=17；
故答案为：17．
点评 主要考查了平行四边形的性质、三角形面积的计算方法；熟练掌握平行四边形的性质，由底和高的关系得出三角形面积之间的关系是解决问题的关键．
练习册系列答案
相关题目
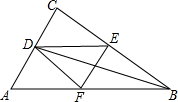如图，Rt△ABC中，∠C=90°，角平分线BD交AC于D，DE∥AB交BC于E，点F为AB上一点，连结DF，EF．已知DC=5，CE=12，则△DEF的面积是（ ）
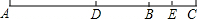如图，已知线段AB，延长AB到点C，使BC=$\frac{1}{4}$AB，点D为AC的中点，点E是BC的中点．
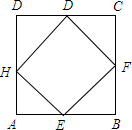如图，长方形EFGH内接于边长为1的正方形ABCD，设AE=x，试求正方形EFGH的面积y与x的函数解析式，写出自变量x的取值范围，并求出AE=$\frac{1}{4}$时，正方形EFGH的面积．
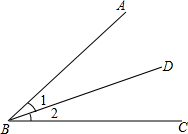如图，