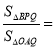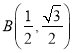题目内容
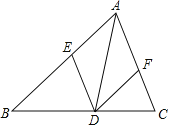
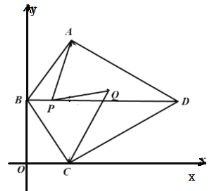
【题目】如图，在四边形
中，
，
，对角线
，点
在
轴上，
与
轴平行，点
在轴上．
（1）求
的度数．
（2）点
在对角线上，点
在四边形内且在点的右边，连接
，已知
，
，设
．
①求
的长（用含
的代数式表示）；
②若某一反比例函数图象同时经过点
、，求的值．
【答案】（1）60°；（2）①
;②
【解析】
（1）连接AC，首先证明
，则有
，进而可得
，再利用勾股定理即可求出BE,DE的长度，然后利用特殊角的三角函数值即可求出
的度数，最后利用
即可求解；
（2）连接AQ，取AD的中点F，连接QF，易证
均为等边三角形，然后证明
，则有
，再证明C,Q,F三点共线，然后求出CF的长度，最后利用
即可求解；
（3）先利用平行线分线段成比例求出Q的坐标，然后求出点A的坐标，进而求出反比例函数的解析式，将Q的坐标代入反比例函数解析式中即可求出m的值．
（1）连接AC交BD于点E，
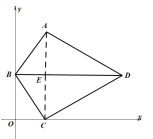
在
和
中，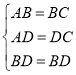
．
，
．
，
设
，
则有
，
解得
．
在
中，
，
，
．
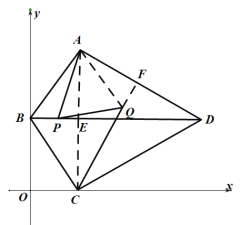
（2）①连接AQ，取AD的中点F，连接QF，
∵
，
，
为等边三角形，
．
∵
，
，
为等边三角形，
，
，
．
，
．
，点F是 AD中点，
．
在
和
中，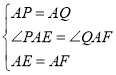
，
．
∵
为等边三角形，点F为AD中点，
，
∴C,Q,F三点共线．
∵
，，
，
；
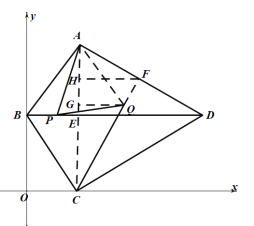
②过点Q作
交AC于点G，过点F作
交AC于点H,
∵
,
．
∵点F是AD中点，
，
．
∵
,
，
，
即
，
解得
，
，
∴点Q的坐标为
．
,
∴点A的坐标为
，
设反比例函数的解析式为
，
将点A代入反比例函数中，得
，
∴反比例函数的解析式为
．
将点Q的坐标代入反比例函数的解析式中，有
，
解得 或
（舍去）．
练习册系列答案
相关题目
