题目内容
17.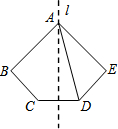 如图所示,五边形ABCDE关于过点A的直线l轴对称,若∠DAE=40°,∠ADE=60°,则∠B的度数为( )
如图所示,五边形ABCDE关于过点A的直线l轴对称,若∠DAE=40°,∠ADE=60°,则∠B的度数为( )| A. | 60° | B. | 40° | C. | 80° | D. | 100° |
分析 利用三角形的内角和等于180°求出∠E,再根据轴对称的性质可得∠B=∠E.
解答 解:∵∠DAE=40°,∠ADE=60°,
∴∠E=180°-∠DAE-∠ADE=180°-40°-60°=80°,
∵五边形ABCDE关于过点A的直线l轴对称,
∴∠B=∠E=80°.
故选C.
点评 本题考查轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.

练习册系列答案
相关题目
8. 如图,直线AB∥CD,AF交CD于点E,∠CEF=135°,则∠A等于( )
如图,直线AB∥CD,AF交CD于点E,∠CEF=135°,则∠A等于( )
 如图,直线AB∥CD,AF交CD于点E,∠CEF=135°,则∠A等于( )
如图,直线AB∥CD,AF交CD于点E,∠CEF=135°,则∠A等于( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
2.下列事件属于不可能事件的是( )
| A. | 抛一次骰子,向上的一面是6点 | B. | 打开电视机,正在转播足球比赛 | ||
| C. | 地球上,向上抛的篮球会下落 | D. | 从只有红球的袋子中,摸出1个白球 |
9.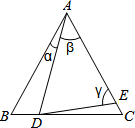 如图,D,E分别是△ABC的边BC,AC上的点,若AB=AC,AD=AE,则( )
如图,D,E分别是△ABC的边BC,AC上的点,若AB=AC,AD=AE,则( )
 如图,D,E分别是△ABC的边BC,AC上的点,若AB=AC,AD=AE,则( )
如图,D,E分别是△ABC的边BC,AC上的点,若AB=AC,AD=AE,则( )| A. | 当∠β为定值时,∠CDE为定值 | B. | 当∠α为定值时,∠CDE为定值 | ||
| C. | 当∠γ为定值时,∠CDE为定值 | D. | ∠CDE的值与∠α,∠β,∠γ的值无关 |
6.当x=$\sqrt{2}$-1时,代数式x2-1的值是( )
| A. | 1 | B. | 2 | C. | 2-$2\sqrt{2}$ | D. | $2\sqrt{2}$-2 |
 如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D做匀速运动,求△ABP的面积S与点P运动的路程x之间的函数关系式及自变量取值范围.
如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D做匀速运动,求△ABP的面积S与点P运动的路程x之间的函数关系式及自变量取值范围.