题目内容
5. 如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D做匀速运动,求△ABP的面积S与点P运动的路程x之间的函数关系式及自变量取值范围.
如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D做匀速运动,求△ABP的面积S与点P运动的路程x之间的函数关系式及自变量取值范围.
分析 运用动点函数进行分段分析,当P在BC上与CD上时,分别求出函数解析式,再结合图象得出符合要求的解析式.
解答 解:①P点在BC上时,BP=x,AB=2,
△ABP的面积S=$\frac{1}{2}$×AB×BP=$\frac{1}{2}$×2x=x,即S=x;
②P点在CD上时,△ABP的高是1,底边是2,所以面积是1,即s=1;
综上所述,S=$\left\{\begin{array}{l}{x(2≤x<3)}\\{1(3≤x≤5)}\end{array}\right.$.
点评 此题主要考查了动点函数的应用,注意将函数分段分析得出解析式是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.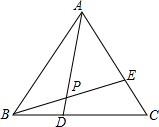 如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )
如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )
 如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )
如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
17.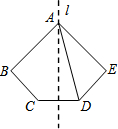 如图所示,五边形ABCDE关于过点A的直线l轴对称,若∠DAE=40°,∠ADE=60°,则∠B的度数为( )
如图所示,五边形ABCDE关于过点A的直线l轴对称,若∠DAE=40°,∠ADE=60°,则∠B的度数为( )
 如图所示,五边形ABCDE关于过点A的直线l轴对称,若∠DAE=40°,∠ADE=60°,则∠B的度数为( )
如图所示,五边形ABCDE关于过点A的直线l轴对称,若∠DAE=40°,∠ADE=60°,则∠B的度数为( )| A. | 60° | B. | 40° | C. | 80° | D. | 100° |
14. 如图,把一根直尺与一块三角板叠放在一起,若∠1=65°,则∠2的度数是( )
如图,把一根直尺与一块三角板叠放在一起,若∠1=65°,则∠2的度数是( )
 如图,把一根直尺与一块三角板叠放在一起,若∠1=65°,则∠2的度数是( )
如图,把一根直尺与一块三角板叠放在一起,若∠1=65°,则∠2的度数是( )| A. | 25° | B. | 35° | C. | 45° | D. | 65° |
15.下列函数中,一次函数有( )
| A. | y=-8x | B. | y=$\frac{-8}{x}$ | C. | y=-8x2+6 | D. | y=-0.5x-1 |