题目内容
如图, ![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 于
于![]()

1.求证:
2.若 ,求
,求 的长.
的长.
1.证明:连接OD、OE
∵∠ABC=90,,∴BC切圆O于点B,∵DE切圆O于点D,∴BE=DE
∵OB=OD,OE=OE
∴△OBE全等于△ODE
∴∠BOE=∠DOE
∴∠BOD=2∠DOE
∵OA=OD
∴∠OAD=∠ODA
∴∠BOD=∠OAD+∠ODA=2∠ODA
∴∠DOE=∠ODA
∴OE∥AC
∵OA=OB
∴DE是△ABC的中位线
∴DE=CE
∴![]()
2.AD=![]()
解析:解析:(2)、解:
∵![]() ,DE=2
,DE=2
∴BC=4
∵tanC=![]()
∴AB/BC=![]() ∴AB=2
∴AB=2![]()
∴AC= =
=![]() =6
=6
∵AB为直径
∴∠ADB=90
∵∠ABC=90, ∠BAD=∠CAB
∴△ABD相似于△ACB
∴AD/AB=AB/AC
∴AD=AB²/AC=(2![]() )²/6=
)²/6=![]()

练习册系列答案
相关题目
 中,
中, ,以
,以 为直径的
为直径的 交
交 于点
于点 ,过点
,过点 于
于


 ,求
,求 的长.
的长.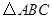 中,
中,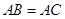 ,以
,以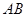 为直径的⊙O交
为直径的⊙O交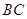 于点
于点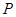 ,
,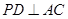 于点
于点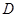 .
.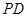 是⊙O的切线;
是⊙O的切线;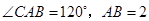 ,求
,求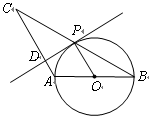
 中,
中,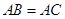 ,以
,以 为直径的⊙O交
为直径的⊙O交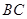 于点
于点 ,
, 于点
于点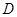 .
.
 中,
中, ,以
,以 为直径的⊙O交
为直径的⊙O交 于点
于点 ,
, 于点
于点 .
.
 中,
中, ,以
,以 为直径的
为直径的 交
交 于点
于点 ,过点
,过点 于
于


 ,求
,求 的长.
的长.