Question

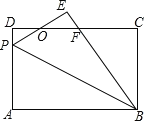
【题目】如图所示，在平面直角坐标系中，，是直角三角形，且，，到轴距离为，把绕点顺时针旋转，得到；把绕点顺时针旋转，得到．以此类推，则旋转第2017次后，得到的直角三角形的直角顶点的坐标为（ ）

A.B.C.D.

Answer 1

【答案】B

【解析】

根据题意可知，在Rt中，可以计算出点的坐标为（1，），由旋转的性质可知，点的横坐标4×2-1=7，纵坐标为，点的横坐标为4×4-1，纵坐标为，由图形规律，依次类推，可以得出点的横坐标为4×2018-1，纵坐标为，计算即可得出结果．

在Rt中，

∵，AB=4，到轴距离为

∴的横坐标为4××=1，点的坐标为（1，），

根据旋转的性质可以得出点的横坐标4×2-1=7，纵坐标为，

由图形规律可得，点的横坐标为4×4-1，纵坐标为，

……，

依次类推，可得点的横坐标为4×2018-1=8071，纵坐标为，

∴点的坐标为（8071，），

故选：B．