题目内容
【题目】鹅岭公园内的小山坡上有一观景楼AB*（如图），山坡BC的坡度为i=1:2.4,为了测量观景楼AB的高度，小楚在山脚C处测得观景楼顶部A的仰角为45°，然后从山脚C沿山坡CB向上行走26米到达E处，测得观景楼顶部A的仰角为72°，（A、B、C、D、E在同一平面内），则观景楼AB的高度约为（ ）米.（结果精确到0.1米，参考数据： 
， 
， 
）
A. 15.6米 B. 18.1米 C. 19.2米 D. 22.5米
【答案】B
【解析】分析：如图，作EF⊥AD于F，作EG⊥CD于G， 
得到
用勾股定理
求出
根据
得到
根据AD=CD,列出方程求出
，利用
求出
即可求解.
详解：如图，作EF⊥AD于F，作EG⊥CD于G，
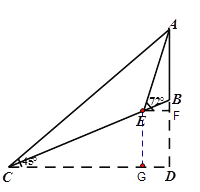
则EF=DG、FD=EG，
∵
即
解得： 
∴FD=EG=10，
设
由
知
∵
∴AD=CD,即
解得：x=7，
AD=CD=31，
解得： 
故选B.
练习册系列答案
优生乐园系列答案
相关题目
