题目内容
【题目】小刘同学在一次课外活动中,用硬纸片做了两个直角三角形,在![]() 中,
中,![]() ,
,![]() ,
,![]() ;在
;在![]() 中,
中,![]() ,
,![]() ,
,![]() .图①是小刘同学所做的一个数学探究:他将
.图①是小刘同学所做的一个数学探究:他将![]() 的直角边
的直角边![]() 与
与![]() 的斜边
的斜边![]() 重合在一起,并将
重合在一起,并将![]() 沿
沿![]() 方向移动.在移动过程中,
方向移动.在移动过程中,![]() 、
、![]() 两点始终在
两点始终在![]() 边上(移动开始时点
边上(移动开始时点![]() 与点
与点![]() 重合).
重合).
(1)在![]() 沿
沿![]() 方向移动的过程中,小刘发现:
方向移动的过程中,小刘发现:![]() 、
、![]() 两点间的距离逐渐 ;连接
两点间的距离逐渐 ;连接![]() 后,
后,![]() 的度数逐渐 .(填“不变”、“变大”或“变小”);
的度数逐渐 .(填“不变”、“变大”或“变小”);
(2)小刘同学经过进一步地研究,编制了如下问题:
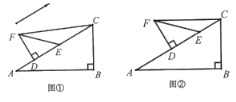
问题①:如图②,当![]() 、
、![]() 的连线与
的连线与![]() 平行时,求平移距离
平行时,求平移距离![]() 的长;
的长;
问题②:如图③,在![]() 的移动过程中,
的移动过程中,![]() 的值是否为定值?如果是,请求出此定值;如果不是,请说明理由.
的值是否为定值?如果是,请求出此定值;如果不是,请说明理由.

【答案】(1)变小;变大;(2)问题①:![]() 时,
时,![]() ; 问题②:
; 问题②:![]() 的值为定值.
的值为定值.![]()
![]()
![]() . 理由见解析.
. 理由见解析.
【解析】
(1)根据题意,观察图形,即可得解.
(2)①因为∠B=90°,∠A=30°,BC=6,所以AC=12,又因为∠FDE=90°,∠DEF=45°,DE=4,所以DF=4,连接FC,设FC∥AB,则可求证∠FCD=∠A=30°,故AD的长可求;
②连接BD、BE,作BH⊥AC于H,根据正弦的概念求出BH的长,求出△BDE的面积,根据S△ADB+S△CEB=△ABC的面积-△BDE的面积计算即可.
(1)变小;变大;
(2)问题①;当![]() 时,
时,![]() ,
,
∴在![]() 中,
中,![]() ,
,
∵在![]() 中,
中,![]() ,
,
∴![]()
∴![]() ,
,
∴![]() 时,
时,![]() ;
;

问题②:![]() 的值为定值.
的值为定值.![]() .
.
理由如下:
如图2,作![]() 于
于![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,
∴![]() 的面积为:
的面积为:![]() ,
,
∴![]()


【题目】如表:方程1、方程2、方程3…是按照一定规律排列的一列方程:
序号 | 方程 | 方程的解 |
1 |
| x1=3,x2=4 |
2 |
| x1=4,x2=6 |
3 |
| x1=5,x2=8 |
… | … | … |
(1)若方程![]() ﹣
﹣![]() =1(a>b)的解是x1=6,x2=10,则a=_____b=_____.
=1(a>b)的解是x1=6,x2=10,则a=_____b=_____.
(2)请写出这列方程中第n个方程:_____ 方程的解:_____.




