题目内容
16.有一道题:“先化简再求值:($\frac{x-1}{x+1}$+$\frac{2x}{{x}^{2}-1}$)÷$\frac{1}{{x}^{2}-1}$,其中x=-$\sqrt{2014}$”,小明做题时把“x=-$\sqrt{2014}$”错抄成了“x=$\sqrt{2014}$”,但他的计算结果仍然正确,请说明理由.分析 先根据分式混合运算的法则把原式进行化简,把x的值代入进行计算即可.
解答 解:原式=$\frac{(x-1)^{2}+2x}{{x}^{2}-1}$÷$\frac{1}{{x}^{2}-1}$
=$\frac{{x}^{2}+1}{{x}^{2}-1}$•(x2-1)
=x2+1.
∵(-$\sqrt{2014}$)2=($\sqrt{2014}$)2,
∴他的计算结果仍然正确.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.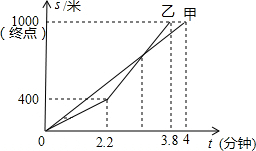 某校运动会上,甲、乙两位同学在1000米比赛时的路程S(米)与时间t(分钟)之间的函数关系如图所示,请你根据图象判断,下列说法正确的是( )
某校运动会上,甲、乙两位同学在1000米比赛时的路程S(米)与时间t(分钟)之间的函数关系如图所示,请你根据图象判断,下列说法正确的是( )
 某校运动会上,甲、乙两位同学在1000米比赛时的路程S(米)与时间t(分钟)之间的函数关系如图所示,请你根据图象判断,下列说法正确的是( )
某校运动会上,甲、乙两位同学在1000米比赛时的路程S(米)与时间t(分钟)之间的函数关系如图所示,请你根据图象判断,下列说法正确的是( )| A. | 甲比乙先到达终点 | |
| B. | 甲比乙多走了200米 | |
| C. | 乙比甲少用了0.2分钟 | |
| D. | 比赛中两人从出发到2.2分钟时间段,乙的速度比甲的速度快 |
8. 如图所示为某几何体的示意图,该几何体的左视图应为( )
如图所示为某几何体的示意图,该几何体的左视图应为( )
 如图所示为某几何体的示意图,该几何体的左视图应为( )
如图所示为某几何体的示意图,该几何体的左视图应为( )| A. |  | B. |  | C. |  | D. |  |
5.下列运算正确的是( )
| A. | 2x+3y=5xy | B. | 5m2•m3=5m5 | C. | (a-b)2=a2-b2 | D. | (m2)3=m5 |
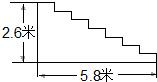 某宾馆在重新装修后,准备在大厅主楼梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图所示,则购买地毯至少需要多少元?
某宾馆在重新装修后,准备在大厅主楼梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图所示,则购买地毯至少需要多少元?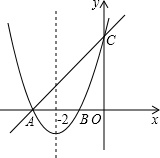 已知:如图,抛物线y1=a(x-h) 2+k与直线y2=k′x+b分别交于x轴和y轴上的点A(-3,0)和点C(0,3),已知抛物线的对称轴为直线x=-2.
已知:如图,抛物线y1=a(x-h) 2+k与直线y2=k′x+b分别交于x轴和y轴上的点A(-3,0)和点C(0,3),已知抛物线的对称轴为直线x=-2.