题目内容
7．
如图所示，河对岸有水塔CD．今在A处测得塔顶C的仰角为30°，前进20米到达B处，又测得C的仰角为45°，则塔高CD的高度为多少？（保留根号）
分析 设CD=x米，根据等腰直角三角形的性质求出BD，根据正切的概念求出AD，结合图形列出方程，解方程即可．
解答 解：设CD=x米，
在Rt△CBD中，∠CBD=45°，
∴BD=CD=x．
在Rt△ACD中，∠CAD=30°，
∴AD=$\sqrt{3}$x．
∵AB=20，
∴AD=x+20．
∴x+20=$\sqrt{3}$x，
解得，x=10（$\sqrt{3}$+1），
答：塔高CD的高度为10（$\sqrt{3}$+1）米．
点评 本题考查俯角、仰角的定义，要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形．
练习册系列答案
相关题目
17．关于二次函数y=-2x2+3，下列说法中正确的是（ ）
| A． | 它的开口方向是向上 | B． | 当x＜-1时，y随x的增大而增大 | ||
| C． | 它的顶点坐标是（-2，3） | D． | 它的对称轴是x=-2 |
如图：列车6258次从福利屯到佳木斯途经笔架山、丰乐镇、太平镇、四马架四个停靠车站，两站之间的距离各不相同，则福利屯至佳木斯和沿途车站售票员应共准备单程15种火车票（假设没有异地售票）．
2．当x=1时，代数式mx3+nx+1的值为2009，当x=-1时，mx3+nx+1的值为（ ）
| A． | -2008 | B． | -2007 | C． | -2009 | D． | 2007 |
12．在下列数：-1.414，-$\sqrt{2}$，$\frac{22}{7}$，111000中，是无理数的是（ ）
| A． | -1.414 | B． | -$\sqrt{2}$ | C． | $\frac{22}{7}$ | D． | 111000 |
19．计算（-2）×3的结果是（ ）
| A． | -5 | B． | -6 | C． | 1 | D． | 6 |
16．
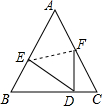如图所示，△ABC是等边三角形，点D为AB上一点，现将△ABC沿EF折叠，使得顶点A与D点重合，且FD⊥BC，则$\frac{AE}{AF}$的值等于（ ）
如图所示，△ABC是等边三角形，点D为AB上一点，现将△ABC沿EF折叠，使得顶点A与D点重合，且FD⊥BC，则$\frac{AE}{AF}$的值等于（ ）| A． | $\frac{4}{3}$ | B． | $\frac{{2\sqrt{3}}}{3}$ | C． | $\frac{{\sqrt{2}+1}}{3}$ | D． | $\frac{{\sqrt{3}+1}}{2}$ |
如图，直线l1，l2分别与另两条直线相交，已知∠1=∠2，求证：∠3+∠4=180°．