题目内容
17.如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC.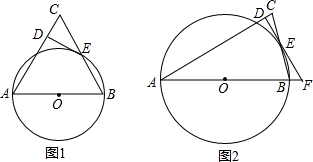
(1)试判断△ABC的形状,并说明理由;
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=2-$\sqrt{3}$,求⊙O的半径和BF的长.
分析 (1)连接OE,根据切线性质得OE⊥DE,与已知中的ED⊥AC得平行,由此得∠1=∠C,再根据同圆的半径相等得∠1=∠B,可得出三角形为等腰三角形;
(2)通过作辅助线构建矩形OGDE,再设与半径有关系的边OG=x,通过AB=AC列等量关系式,可求得结论.
解答  解:(1)△ABC是等腰三角形,理由是:
解:(1)△ABC是等腰三角形,理由是:
如图1,连接OE,
∵DE是⊙O的切线,
∴OE⊥DE,
∵ED⊥AC,
∴AC∥OE,
∴∠1=∠C,
∵OB=OE,
∴∠1=∠B,
∴∠B=∠C,
∴△ABC是等腰三角形;
(2)如图2,过点O作OG⊥AC,垂足为G,则得四边形OGDE是矩形, ∵△ABC是等腰三角形,
∵△ABC是等腰三角形,
∴∠B=∠C=75°,
∴∠A=180°-75°-75°=30°,
设OG=x,则OA=OB=OE=2x,AG=$\sqrt{3}$x,
∴DG=OE=2x,
根据AC=AB得:4x=$\sqrt{3}$x+2x+2-$\sqrt{3}$,
x=1,
∴OE=OB=2,
在直角△OEF中,∠EOF=∠A=30°,
cos30=$\frac{OE}{OF}$,OF=$\frac{2}{cos30}$=2÷$\frac{\sqrt{3}}{2}$=$\frac{4\sqrt{3}}{3}$,
∴BF=$\frac{4\sqrt{3}}{3}$-2,⊙O的半径为2.
点评 本题考查了切线的性质,由定理可知,若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系,由此得出平行和角的关系,根据两个角相等的三角形是等腰三角形可得△ABC是等腰三角形;第二问运用了直角三角形30°角的性质及等腰三角形和矩形的有关性质,关键是找出恰当的等量关系式:AC=AB,设未知数,列关于x的一元一次方程得出结论.

练习册系列答案
相关题目
8.函数y=$\frac{\sqrt{x+2}}{x}$的自变量x的取值范围是( )
| A. | x≥-2 | B. | x≥-2且x≠0 | C. | x≠0 | D. | x>0且x≠-2 |
9.甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
(1)分别计算甲、乙成绩的中位数;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
| 数与代数 | 空间与图形 | 统计与概率 | 综合与实践 | |
| 学生甲 | 90 | 93 | 89 | 90 |
| 学生乙 | 94 | 92 | 94 | 86 |
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
7.下列图案中既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,⊙O是△ABC的外接圆,直径AD=4,∠ABC=∠DAC,则AC长为2$\sqrt{2}$.
如图,⊙O是△ABC的外接圆,直径AD=4,∠ABC=∠DAC,则AC长为2$\sqrt{2}$.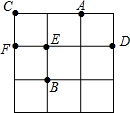 如图,在3×3的方格中,A、B、C、D、E、F分别位于格点上,从C、D、E、F四点中任取一点,与点A、B为顶点作三角形,则所作三角形为等腰三角形的概率是$\frac{3}{4}$.
如图,在3×3的方格中,A、B、C、D、E、F分别位于格点上,从C、D、E、F四点中任取一点,与点A、B为顶点作三角形,则所作三角形为等腰三角形的概率是$\frac{3}{4}$.