题目内容
如图1,已知tan∠MON=2,点P是∠MON内一点,PC⊥OM,垂足为点C,PC=2,OC=6,A是OC延长线上一点,连接AP并延长与射线ON交于点B.(1)当点P恰好是线段AB的中点时,试判断△AOB的形状,并说明理由;
(2)当CA的长度为多少时,△AOB是等腰三角形;
(3)设
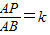 ,是否存在适当的k,使得
,是否存在适当的k,使得 ?若存在,试求出k的值;若不存在,试说明理由.
?若存在,试求出k的值;若不存在,试说明理由.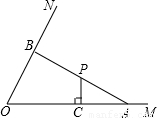
【答案】分析:(1)过点B作BE⊥OM,垂足为点E,根据中位线的性质得到BE=4,再根据正切的定义得到OE=2,EC=CA=4,易证得Rt△OBE≌Rt△PAC,得到∠OBE=∠OAB,∠AOB=∠CPA,而∠CPA=∠EBA,即可得到∠OBE+∠EBA=90°;
(2)设OE=a,则BE=2a,OB= a,设CA=x,由PC∥BE,则
a,设CA=x,由PC∥BE,则 ,可得到a=
,可得到a= ,然后分类讨论:若OA=OB,即x+6=
,然后分类讨论:若OA=OB,即x+6= •
• ;若AO=AB,即
;若AO=AB,即 ;若OB=AB时,OE=EA,
;若OB=AB时,OE=EA, ,分别解方程即可得到x的值;
,分别解方程即可得到x的值;
(3)同(2)设法一样,根据三角形的面积公式得到S△APC= •x•2=x,S△ABO=
•x•2=x,S△ABO= •2a•(x+6)=(x+6)a,由
•2a•(x+6)=(x+6)a,由 ,得
,得 =
= =
= ,得到
,得到 ,再根据题意得到
,再根据题意得到
 ,而a=
,而a= ,即可得到关于x的方程,解方程即可.
,即可得到关于x的方程,解方程即可.
解答: 解:(1)△AOB为直角三角形.理由如下:
解:(1)△AOB为直角三角形.理由如下:
过点B作BE⊥OM,垂足为点E,如图,
∵PC⊥OM,
∴BE∥PC,
∵点P是线段AB的中点,PC=2,
∴BE=4,
又∵tan∠MON=2,tan∠MON= =2,
=2,
∴OE=2,
∵OC=6,
∴EC=CA=4
∴Rt△OBE≌Rt△PAC,
∴∠OBE=∠OAB,∠AOB=∠CPA,
而∠CPA=∠EBA,
∴∠OBE+∠EBA=90°,
∴△OBA为直角三角形;
(2)设OE=a,则BE=2a,OB= a
a
∵PC∥BE,
∴ ,
,
设CA=x,则 =
= ,
,
∴a= ,
,
∴OA=6+x,OB= ,
,
①若OA=OB,即x+6= •
•
解得x= -1;
-1;
②若AO=AB,即
解得 ;
;
③若OB=AB时,OE=EA,
∴ ,解得x=1;
,解得x=1;
综上,当CA的值分别为 、
、 、1时,△AOB是等腰三角形.
、1时,△AOB是等腰三角形.
(3)存在.理由如下:
同(2)设CA=x,OE=a,
∵S△APC= •x•2=x,S△ABO=
•x•2=x,S△ABO= •2a•(x+6)=(x+6)a,
•2a•(x+6)=(x+6)a,
由 ,得
,得 =
= =
= ,
,
∴ ,
,
∵ ,
,
∴ ,
,
∴x=6a,
而a= ,
,
∴6• =x,
=x,
解得x1=9,x2=-4(舍去),
∴ .
.
点评:本题考查了相似三角形的判定与性质:平行于三角形一边的直线所截得的三角形与原三角形相似;相似三角形对应边的比等于相似比.也考查了三角形的中位线定理以及解方程的方法.
(2)设OE=a,则BE=2a,OB=
 a,设CA=x,由PC∥BE,则
a,设CA=x,由PC∥BE,则 ,可得到a=
,可得到a= ,然后分类讨论:若OA=OB,即x+6=
,然后分类讨论:若OA=OB,即x+6= •
• ;若AO=AB,即
;若AO=AB,即 ;若OB=AB时,OE=EA,
;若OB=AB时,OE=EA, ,分别解方程即可得到x的值;
,分别解方程即可得到x的值;(3)同(2)设法一样,根据三角形的面积公式得到S△APC=
 •x•2=x,S△ABO=
•x•2=x,S△ABO= •2a•(x+6)=(x+6)a,由
•2a•(x+6)=(x+6)a,由 ,得
,得 =
= =
= ,得到
,得到 ,再根据题意得到
,再根据题意得到 ,而a=
,而a= ,即可得到关于x的方程,解方程即可.
,即可得到关于x的方程,解方程即可.解答:
 解:(1)△AOB为直角三角形.理由如下:
解:(1)△AOB为直角三角形.理由如下:过点B作BE⊥OM,垂足为点E,如图,
∵PC⊥OM,
∴BE∥PC,
∵点P是线段AB的中点,PC=2,
∴BE=4,
又∵tan∠MON=2,tan∠MON=
 =2,
=2,∴OE=2,
∵OC=6,
∴EC=CA=4
∴Rt△OBE≌Rt△PAC,
∴∠OBE=∠OAB,∠AOB=∠CPA,
而∠CPA=∠EBA,
∴∠OBE+∠EBA=90°,
∴△OBA为直角三角形;
(2)设OE=a,则BE=2a,OB=
 a
a∵PC∥BE,
∴
 ,
,设CA=x,则
 =
= ,
,∴a=
 ,
,∴OA=6+x,OB=
 ,
,①若OA=OB,即x+6=
 •
•
解得x=
 -1;
-1;②若AO=AB,即

解得
 ;
;③若OB=AB时,OE=EA,
∴
 ,解得x=1;
,解得x=1;综上,当CA的值分别为
 、
、 、1时,△AOB是等腰三角形.
、1时,△AOB是等腰三角形.(3)存在.理由如下:
同(2)设CA=x,OE=a,
∵S△APC=
 •x•2=x,S△ABO=
•x•2=x,S△ABO= •2a•(x+6)=(x+6)a,
•2a•(x+6)=(x+6)a,由
 ,得
,得 =
= =
= ,
,∴
 ,
,∵
 ,
,∴
 ,
,∴x=6a,
而a=
 ,
,∴6•
 =x,
=x,解得x1=9,x2=-4(舍去),
∴
 .
.点评:本题考查了相似三角形的判定与性质:平行于三角形一边的直线所截得的三角形与原三角形相似;相似三角形对应边的比等于相似比.也考查了三角形的中位线定理以及解方程的方法.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 在地面上以点B为圆心、AB长为半径的圆形区域为危险区域,精确到0.1m)
在地面上以点B为圆心、AB长为半径的圆形区域为危险区域,精确到0.1m)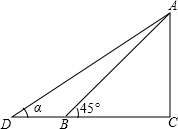 某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由45°改为α(如图),已知
某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由45°改为α(如图),已知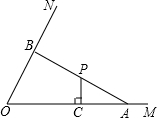 长线上一点,连接AP并延长与射线ON交于点B.
长线上一点,连接AP并延长与射线ON交于点B.