题目内容
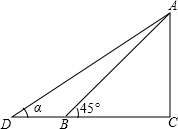 某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由45°改为α(如图),已知tanα=
某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由45°改为α(如图),已知tanα=| 3 |
| 4 |
| 2 |
| 3 |
| 6 |
分析:利用图中△ABC已知条件分别求得BC、AC长,进而利用∠α的tan值求得CD长,再利用勾股定理求得AD长即可求解.
解答:解:∵在Rt△ABC中,∠C=90°,∠ABC=45°,AB=6,
∴AC=BC=3
.
∵tanα=
,
∴
=
.
∴DC=4
.
∵在Rt△ADC中,∠C=90°,AC=3
,DC=4
,
∴AD=5
.
∴AD-AB=5
-6=1.07≈1.1.
答:改善后滑滑板会加长约1.1米.
∴AC=BC=3
| 2 |
∵tanα=
| 3 |
| 4 |
∴
| AC |
| DC |
| 3 |
| 4 |
∴DC=4
| 2 |
∵在Rt△ADC中,∠C=90°,AC=3
| 2 |
| 2 |
∴AD=5
| 2 |
∴AD-AB=5
| 2 |
答:改善后滑滑板会加长约1.1米.
点评:本题考查锐角三角函数的应用.

练习册系列答案
相关题目
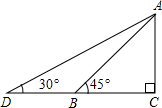 如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由45°降为30°,已知AC=5米,点D、B、C在同一水平地面上.
如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由45°降为30°,已知AC=5米,点D、B、C在同一水平地面上. (2013•鞍山)如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾斜度由45°降为
(2013•鞍山)如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾斜度由45°降为 (2013•保康县二模)如图,某幼儿园为了加强安全管理,决定将幼儿园内的滑梯的倾角由45°改为30°,已知原滑梯AB的长为5米,在高度不变的情况下,新滑梯长为AD,点D、B、C 在同一水平地面上.
(2013•保康县二模)如图,某幼儿园为了加强安全管理,决定将幼儿园内的滑梯的倾角由45°改为30°,已知原滑梯AB的长为5米,在高度不变的情况下,新滑梯长为AD,点D、B、C 在同一水平地面上. (2013•襄城区模拟)如图所示,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾斜角由45°降为30°,已知原滑滑板AB的长为5米,点D、B、C在同一水平地面上.若滑滑板的正前方能有3米长的空地就能保证安全,原滑滑板的前方有6米长的空地,像这样改造是否可行?请说明理由.(参考数据:
(2013•襄城区模拟)如图所示,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾斜角由45°降为30°,已知原滑滑板AB的长为5米,点D、B、C在同一水平地面上.若滑滑板的正前方能有3米长的空地就能保证安全,原滑滑板的前方有6米长的空地,像这样改造是否可行?请说明理由.(参考数据: