题目内容
开口向下的抛物线y=(m2-2)x2+3mx+1的对称轴经过点(-1,3),则m= .
考点:二次函数的性质
专题:
分析:根据对称轴经过的点可以确定抛物线的对称轴,从而得到有关m的方程,求解即可.
解答:解:由于抛物线y=(m2-2)x2+3mx+1的对称轴经过点(-1,3),
∴对称轴为直线x=-1,x=-
=-1,
解得m1=
,m2=
.
由于抛物线的开口向下,所以当m=
时,m2-2>0,不合题意,应舍去,
∴m=
.
故答案为:
.
∴对称轴为直线x=-1,x=-
| 3m |
| 2(m2-2) |
解得m1=
3+
| ||
| 4 |
3-
| ||
| 4 |
由于抛物线的开口向下,所以当m=
3+
| ||
| 4 |
∴m=
3-
| ||
| 4 |
故答案为:
3-
| ||
| 4 |
点评:此题考查了二次函数的性质,了解抛物线的对称轴公式是解答本题的关键.

练习册系列答案
相关题目
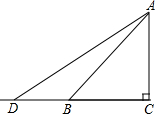 如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB的长为15m,它的坡角为45°,为了提高该堤的防洪能力,现将背水坡改造成坡度为1:1.6的斜坡AD.在CB方向距B处5m处有一座房屋,问在背水坡改造的施工过程中,此处房屋是否需要拆除?
如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB的长为15m,它的坡角为45°,为了提高该堤的防洪能力,现将背水坡改造成坡度为1:1.6的斜坡AD.在CB方向距B处5m处有一座房屋,问在背水坡改造的施工过程中,此处房屋是否需要拆除?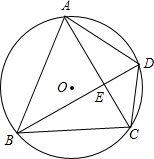 如图,四边形ABCD是⊙O的内接四边形,AC⊥BD,垂足为E,CE:BE=1:2,CD=5,求⊙O的直径.
如图,四边形ABCD是⊙O的内接四边形,AC⊥BD,垂足为E,CE:BE=1:2,CD=5,求⊙O的直径. 如图,在半径为10cm的圆中作一个正六边形ABCDEF,试求此正六边形的面积.
如图,在半径为10cm的圆中作一个正六边形ABCDEF,试求此正六边形的面积.