题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
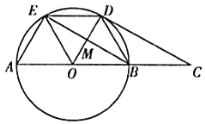
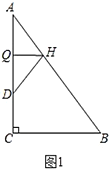
(1)如图1,折叠![]() 使点
使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕交
处,折痕交![]() 、
、![]() 分别于点
分别于点![]() 、
、![]() ,若
,若![]() ,则
,则![]() ________.
________.
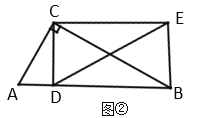
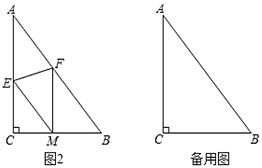
(2)如图2,折叠![]() 使点
使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕交
处,折痕交![]() 、
、![]() 分别于点
分别于点![]() 、
、![]() .若
.若![]() ,求证:四边形
,求证:四边形![]() 是菱形;
是菱形;
(3)在(1)(2)的条件下,线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 和
和![]() 相似?若存在,求出
相似?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)5;(2)见解析;(3)存在,满足条件长![]() 的值为
的值为![]() 或10或
或10或![]() .
.
【解析】
(1)利用勾股定理求出AC,设HQ=x,根据![]() ,构建方程即可解决问题;
,构建方程即可解决问题;
(2)由翻折的性质可得![]() ,
,![]() ,然后证明出
,然后证明出![]() 即可;
即可;
(3)设AE=EM=FM=AF=4m,则BM=3m,FB=5m,构建方程求出m的值,然后根据![]() ,
,![]() ,求出
,求出![]() ,设
,设![]() ,分两种情形分别求解即可解决问题.
,分两种情形分别求解即可解决问题.
解:(1)在![]() 中,∵
中,∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 或-5(舍弃),
或-5(舍弃),
∴![]() ,
,
故答案为5;
(2)由翻折的性质可知:![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是菱形;
是菱形;
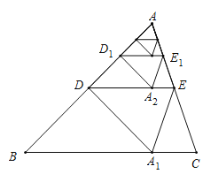
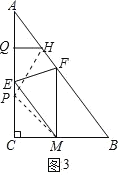
(3)如图3中,设![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,
,
当![]() 时,
时,![]() ,
,
∴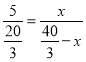 ,解得:
,解得:![]() ,
,
当![]() 时,
时,![]() ,
,
∴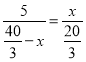 ,解得:
,解得:![]() 或
或![]() ,
,
经检验:![]() 或
或![]() 是分式方程的解,且符合题意,
是分式方程的解,且符合题意,
综上所述,满足条件的![]() 的长为
的长为![]() 或10或
或10或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某市对即将参加中考的4000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图.请根据图表信息回答下列问题:
初中毕业生视力抽样调查频数分布表
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |

(1)本次调查样本容量为 ;
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均属标准视力,根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人?