题目内容
 如图,半径为R的⊙O的弦AC=BD,AC、BD交于E,F为
如图,半径为R的⊙O的弦AC=BD,AC、BD交于E,F为 |
| BC |
| 2 |
 |
| CF |
 |
| CD |
| 2 |
分析:①由弦AC=BD,可得
=
,继而可得
=
,然后由圆周角定理,证得∠ABD=∠BAC,即可判定AE=BE;
②连接OA,OD,由AE=BE,AC⊥BD,可求得∠ABD=45°,继而可得△AOD是等腰直角三角形,则可求得AD=
R;
③设AF与BD相交于点G,连接CG,易证得△BGF是等腰三角形,CE=DE=EG,继而求得答案.
 |
| AC |
 |
| BD |
 |
| BC |
 |
| AD |
②连接OA,OD,由AE=BE,AC⊥BD,可求得∠ABD=45°,继而可得△AOD是等腰直角三角形,则可求得AD=
| 2 |
③设AF与BD相交于点G,连接CG,易证得△BGF是等腰三角形,CE=DE=EG,继而求得答案.
解答:解:①∵弦AC=BD,
∴
=
,
∴
=
,
∴∠ABD=∠BAC,
∴AE=BE;
②连接OA,OD,
∵AC⊥BD,AE=BE,
∴∠ABE=∠BAE=45°,
∴∠AOD=2∠ABE=90°,
∵OA=OD,
∴AD=
R;
③设AF与BD相交于点G,连接CG,
∵
=
,
∴∠FAC=∠DAC,
∵AC⊥BD,
∵在△AGE和△ADE中,
,
 ∴△AGE≌△ADE(ASA),
∴△AGE≌△ADE(ASA),
∴AG=AD,EG=DE,
∴∠AGD=∠ADG,
∵∠BGF=∠AGD,∠F=∠ADG,
∴∠BGF=∠F,
∴BG=BF,
∵AC=BD,AE=BE,
∴DE=CE,
∴EG=CE,
∴BE=BG+EG=BF+CE,
∵AB=
,
∴BE=AB•cos45°=1,
∴BF+CE=1.
故其中正确的是:①②③.
故选D.
∴
 |
| AC |
 |
| BD |
∴
 |
| BC |
 |
| AD |
∴∠ABD=∠BAC,
∴AE=BE;
②连接OA,OD,
∵AC⊥BD,AE=BE,
∴∠ABE=∠BAE=45°,
∴∠AOD=2∠ABE=90°,
∵OA=OD,
∴AD=
| 2 |
③设AF与BD相交于点G,连接CG,
∵
 |
| CF |
 |
| CD |
∴∠FAC=∠DAC,
∵AC⊥BD,
∵在△AGE和△ADE中,
|
 ∴△AGE≌△ADE(ASA),
∴△AGE≌△ADE(ASA),∴AG=AD,EG=DE,
∴∠AGD=∠ADG,
∵∠BGF=∠AGD,∠F=∠ADG,
∴∠BGF=∠F,
∴BG=BF,
∵AC=BD,AE=BE,
∴DE=CE,
∴EG=CE,
∴BE=BG+EG=BF+CE,
∵AB=
| 2 |
∴BE=AB•cos45°=1,
∴BF+CE=1.
故其中正确的是:①②③.
故选D.
点评:此题考查了圆周角定理、弧与弦的关系、等腰直角三角形的性质与判定以及全等三角形的判定与性质等知识.此题难度较大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图,半径为1的⊙D内切于圆心角为60°的扇形OAB,
如图,半径为1的⊙D内切于圆心角为60°的扇形OAB,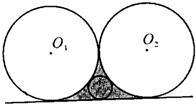 12、如图,半径为4的两等圆相外切,它们的一条外公切线与两圆围成的阴影部分中,存在的最大圆的半径等于
12、如图,半径为4的两等圆相外切,它们的一条外公切线与两圆围成的阴影部分中,存在的最大圆的半径等于 如图,半径为30km 的圆A是环保部分划定的生态保护区,B、C是位于保护区附近相距100km的两城市.如果在 B、C两城之间修一条笔直的公路,经测量∠ABC=45°,∠ACB=30°.
如图,半径为30km 的圆A是环保部分划定的生态保护区,B、C是位于保护区附近相距100km的两城市.如果在 B、C两城之间修一条笔直的公路,经测量∠ABC=45°,∠ACB=30°. 如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为
如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为 (2013•高淳县一模)如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A、B,与⊙O1分别交于C、D,则弧APB与弧CPD的长度之和为
(2013•高淳县一模)如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A、B,与⊙O1分别交于C、D,则弧APB与弧CPD的长度之和为