题目内容
在平面直角坐标系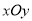 中,
中, 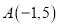 ,
, 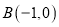 ,
, 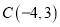 .
.
( )求出
)求出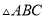 的面积.
的面积.
( )在图中作出
)在图中作出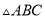 关于
关于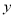 轴的对称图形
轴的对称图形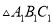 并写出点
并写出点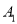 ,
, 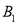 ,
, 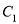 的坐标.
的坐标.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
题目内容
在平面直角坐标系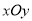 中,
中, 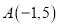 ,
, 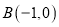 ,
, 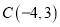 .
.
(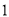 )求出
)求出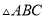 的面积.
的面积.
(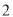 )在图中作出
)在图中作出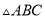 关于
关于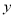 轴的对称图形
轴的对称图形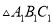 并写出点
并写出点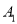 ,
, 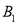 ,
, 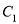 的坐标.
的坐标.

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案