题目内容
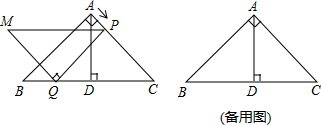
12. 已知:如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O,点P从点A出发,沿AD方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6),解答下列问题:
已知:如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O,点P从点A出发,沿AD方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6),解答下列问题:(1)当t为何值时,AP=PO.
(2)设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使OD平分∠COP?若存在,求出t的值;若不存在,请说明理由.
分析 (1)根据矩形的性质和勾股定理得到AC=10,过P作PM⊥AO,证明△APM∽△ACD,根据相似三角形的性质即可得出答案;
(2)过点O作OH⊥BC交BC于点H,已知BE=PD,则可求△BOE的面积;可证得△DFQ∽△DOC,由相似三角形的面积比可求得△DFQ的面积,从而可求五边形OECQF的面积.
(3)由角平分线的性质得到DM=DN=$\frac{24}{5}$,根据勾股定理得到ON=OM=$\sqrt{O{D}^{2}-D{N}^{2}}$=$\frac{7}{5}$,由三角形的面积公式得到OP=5-$\frac{5}{8}$t,根据勾股定理列方程,解方程即可得到结论.
解答 解:(1)∵在矩形ABCD中,AB=6cm,BC=8cm,∠ABC=90°,
∴AC=10,AO=$\frac{1}{2}$AC=5,
∵AP=PO=t,
过P作PM⊥AO,如图1所示:
∴AM=$\frac{1}{2}$AO=$\frac{5}{2}$,
∵∠PMA=∠ADC=90°,∠PAM=∠CAD,
∴△APM∽△ACD,
∴$\frac{AP}{AC}=\frac{AM}{AD}$,即$\frac{t}{10}=\frac{\frac{5}{2}}{8}$,
解得:t=$\frac{25}{8}$,
即t=$\frac{25}{8}$时,AP=PO;
(2)过点O作OH⊥BC交BC于点H,则OH=$\frac{1}{2}$CD=$\frac{1}{2}$AB=3cm.
由矩形的性质可知∠PDO=∠EBO,DO=BO,
在△DOP和△BOE中,$\left\{\begin{array}{l}{∠PDO=∠EBO}&{\;}\\{OD=OB}&{\;}\\{∠DOP=∠BOE}&{\;}\end{array}\right.$,
∴△DOP≌BOE(ASA),
∴BE=PD=8-t,
则S△BOE=$\frac{1}{2}$BE•OH=$\frac{1}{2}$×3(8-t)=12-$\frac{3}{2}$t.
∵FQ∥AC,
∴△DFQ∽△DOC,相似比为$\frac{DQ}{DC}=\frac{t}{6}$,
∴$\frac{{S}_{△DFQ}}{{S}_{△DOC}}$=$\frac{{t}^{2}}{36}$,
∵S△DOC=$\frac{1}{4}$S矩形ABCD=$\frac{1}{4}$×6×8=12cm2,
∴S△DFQ=12×$\frac{{t}^{2}}{36}$=$\frac{{t}^{2}}{3}$,
∴S五边形OECQF=S△DBC-S△BOE-S△DFQ=$\frac{1}{2}$×6×8-(12-$\frac{3}{2}$t)-$\frac{{t}^{2}}{3}$=-$\frac{1}{3}$t2+$\frac{3}{2}$t+12;
∴S与t的函数关系式为S=-$\frac{1}{3}$t2+$\frac{3}{2}$t+12;
(3)存在,理由如下:
如图3,过D作DM⊥PE于M,DN⊥AC于N,
∵∠POD=∠COD,
∴DM=DN=$\frac{24}{5}$,
∴ON=OM=$\sqrt{O{D}^{2}-D{N}^{2}}$=$\frac{7}{5}$,
∵OP•DM=3PD,
∴OP=5-$\frac{5}{8}$t,
∴PM=$\frac{18}{5}$-$\frac{5}{8}$t,
∵PD2=PM2+DM2,
∴(8-t)2=($\frac{18}{5}$-$\frac{5}{8}$t)2+($\frac{24}{5}$)2,
解得:t=16(不合题意,舍去),t=$\frac{112}{39}$,
∴当t=$\frac{112}{39}$时,OD平分∠COP.
点评 本题是四边形综合题目,考查了矩形的性质,角平分线的性质,相似三角形的判定和性质,图形面积的计算,全等三角形的判定和性质、勾股定理等知识;本题综合性强,有一定难度,证明三角形全等和三角形相似是解决问题的关键.

| A. | x-y2=2 | B. | 3x+2y=1 | C. | $\frac{1}{x}$=y+1 | D. | $\frac{x}{2}$+5y |
| A. | (a-3)2=a2-9 | B. | a2•a4=a8 | C. | $\sqrt{9}$=±3 | D. | x6÷x3=x3 |
| A. | 由5x=-4得x=-$\frac{5}{4}$ | B. | 由4x+2=3x-1得4x+3x=2-1 | ||
| C. | 由$\frac{x}{5}$-1=2得x-5=2 | D. | 由4x-3=2x-2得2x=1 |
| A. | (2x+y)(2x-y) | B. | (x-y)(y-x) | C. | (-x+y)(-x-y) | D. | (x+y)(-x+y) |
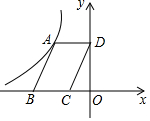 如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过A作?ABCD,使点B在x轴上,点D在y轴上,已知?ABCD的面积为6,则k的值为( )
如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过A作?ABCD,使点B在x轴上,点D在y轴上,已知?ABCD的面积为6,则k的值为( )