题目内容
18.(1)计算:($\frac{1}{2}$)-1+(5+$\sqrt{3}$)0-2sin45°+$\frac{1}{\sqrt{2}+1}$.(2)解方程:x2-4x+1=0.
分析 (1)先根据负整数指数幂、零指数幂、特殊角的三角函数值、分母有理化分别求出每一部分的值,再代入求出即可;
(2)先移项,配方,开方,即可得出两个方程,求出方程的解即可.
解答 解:(1)原式=2+1-2×$\frac{\sqrt{2}}{2}$+$\sqrt{2}$-1
=2;
(2)x2-4x+1=0,
x2-4x=-1,
x2-4x+4=-1+4,
(x-2)2=3,
x-2=$±\sqrt{3}$,
x1=2+$\sqrt{3}$,x2=2-$\sqrt{3}$.
点评 本题考查了负整数指数幂、零指数幂、特殊角的三角函数值、分母有理化和解一元二次方程,能求出每一部分的值和选择适当的方法解方程是解此题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
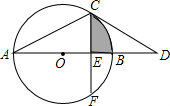 如图,已知⊙O 中,AB为直径,CD为⊙O的切线,交AB的延长线于点D,∠D=30°.
如图,已知⊙O 中,AB为直径,CD为⊙O的切线,交AB的延长线于点D,∠D=30°. 已知:如图所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.求证:①BE=CD;②△AMN是等腰三角形.
已知:如图所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.求证:①BE=CD;②△AMN是等腰三角形.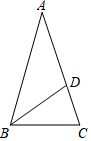 如图,△ABC中,AB=AC,D是AC上的一点,CD=5,BC=13,BD=12.
如图,△ABC中,AB=AC,D是AC上的一点,CD=5,BC=13,BD=12.