题目内容
10.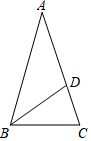 如图,△ABC中,AB=AC,D是AC上的一点,CD=5,BC=13,BD=12.
如图,△ABC中,AB=AC,D是AC上的一点,CD=5,BC=13,BD=12.(1)判断△ADB的形状,并说明理由.
(2)点A到BC边的距离为15.6.
分析 (1)根据题意计算出CD2+BD2和BC2,根据勾股定理的逆定理判断即可;
(2)设AB=x,根据勾股定理列出方程,解方程即可.
解答 解:(1)CD2+BD2=25+144=169,
BC2=169,
∴CD2+BD2=BC2,
∴△BCD是直角三角形;
(2)设AB=x,则AC=x,AD=x-5,
由勾股定理得,x2=(x-5)2+122,
∴x=16.9,
∴AC=16.9,
由(1)知S△ABC=$\frac{1}{2}$AC•BD,
设点A到BC边的距离为h,则S△ABC=$\frac{1}{2}$h•BC,
∴AC•BD=h•BC,
∴h=$\frac{AC•BD}{BC}$=$\frac{16.9×12}{13}$=15.6,
∴点A到BC边的距离为15.6,
故答案为:15.6.
点评 本题考查的是勾股定理及其逆定理的应用,掌握如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形是解题的关键.

练习册系列答案
相关题目
5.如果水位下降3m,记作+3m,那么水位上升4m,记作( )
| A. | 1m | B. | 7m | C. | 4m | D. | -4m |
19.解关于x的方程-3x-9=$\frac{1}{2}$x+5,下面的变形正确的是( )
| A. | -3x+$\frac{1}{2}$x=5-9 | B. | -3x-$\frac{1}{2}$x=(-9)+(-5) | C. | $\frac{1}{2}$x+3x=(-9)+(-5) | D. | $\frac{1}{2}$x+3x=5+9 |
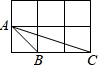 如图,每个小正方形边长均为1,则下列图中的阴影三角形与如图所示的△ABC相似的是( )
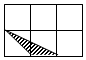
如图,每个小正方形边长均为1,则下列图中的阴影三角形与如图所示的△ABC相似的是( )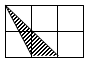
 如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.请完整填上结论或依据.
如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.请完整填上结论或依据.