题目内容
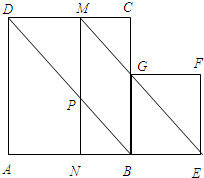
 设正方形ABCD的边CD的中点为E,F是CE的中点(图).求证:
设正方形ABCD的边CD的中点为E,F是CE的中点(图).求证: .
.
 证明:如图,作∠BAF的平分线AH交DC的延长线于H,则∠1=∠2=∠3,
证明:如图,作∠BAF的平分线AH交DC的延长线于H,则∠1=∠2=∠3,所以FA=FH.
设正方形边长为a,在Rt△ADF中,
AF2=AD2+DF2=a2+
 =
= a2,
a2,所以AF=
 =FH.
=FH.从而CH=FH-FC=
 -
- =a,
=a,所以Rt△ABG≌Rt△HCG(AAS),GB=GC=DE=
 a.
a.从而Rt△ABG≌Rt△ADE(SAS),
所以∠DAE=∠2=
 ∠BAF.
∠BAF.分析:作∠BAF的平分线,将角分为∠1与∠2相等的两部分,设法证明∠DAE=∠1或∠2即可,求证Rt△ABG≌Rt△ADE即可得∠DAE=∠2.
点评:本题考查了勾股定理在直角三角形中的运用,考查了全等三角形的判定和对应边相等性质,本题中正确的求Rt△ABG≌Rt△ADE是解题的关键.

练习册系列答案
相关题目
 BE的长.
BE的长. 设正方形ABCD的边CD的中点为E,F是CE的中点(图).求证:
设正方形ABCD的边CD的中点为E,F是CE的中点(图).求证: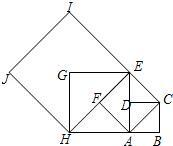 如图,设正方形ABCD的边长为2,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,根据以上规律写出的表达式:an=
如图,设正方形ABCD的边长为2,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,根据以上规律写出的表达式:an=
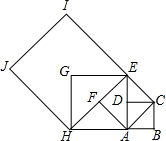 设正方形ABCD的边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…记正方形ABCD的边长为a1=1,按上述方法作出的正方形的边长依次为a2,a3,a4,…,an,请求出a2,a3,a4的值;根据以上规律写出an的表达式
设正方形ABCD的边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…记正方形ABCD的边长为a1=1,按上述方法作出的正方形的边长依次为a2,a3,a4,…,an,请求出a2,a3,a4的值;根据以上规律写出an的表达式