题目内容
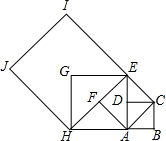 设正方形ABCD的边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…记正方形ABCD的边长为a1=1,按上述方法作出的正方形的边长依次为a2,a3,a4,…,an,请求出a2,a3,a4的值;根据以上规律写出an的表达式
设正方形ABCD的边长为1的正方形,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…记正方形ABCD的边长为a1=1,按上述方法作出的正方形的边长依次为a2,a3,a4,…,an,请求出a2,a3,a4的值;根据以上规律写出an的表达式an=(
)n-1
| 2 |
an=(
)n-1
.| 2 |
分析:根据第一个正方形的边长为1可以求得第二个正方形的边长,以此类推可以求得正方形的边长满足一定的规律,根据次规律可以求得第n个正方形的边长.
解答:解:∵正方形ABCD的边长为1的正方形,
∴a1=1=(
)0,
∵AC是正方形ABCD的对角线,
∴AC=
,
∴a2=
=
,
同理可得
a3=
=2=(
)2
a4=
=2
=(
)3,
…
∴an=(
)n-1.
故答案为:2n-1.
∴a1=1=(
| 2 |
∵AC是正方形ABCD的对角线,
∴AC=
| 2 |
∴a2=
| 12+12 |
| 2 |
同理可得
a3=
(
|
| 2 |
a4=
| (2)2+(2)2 |
| 2 |
| 2 |
…
∴an=(
| 2 |
故答案为:2n-1.
点评:本题考查了正方形的性质及勾股定理的知识,解题的关键是根据正方形的性质及勾股定理总结出正方形的边长满足的规律.

练习册系列答案
相关题目
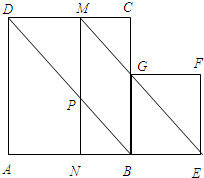 BE的长.
BE的长. 设正方形ABCD的边CD的中点为E,F是CE的中点(图).求证:
设正方形ABCD的边CD的中点为E,F是CE的中点(图).求证: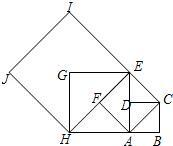 如图,设正方形ABCD的边长为2,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,根据以上规律写出的表达式:an=
如图,设正方形ABCD的边长为2,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,根据以上规律写出的表达式:an=