Question

二次函数y=x²的图象如图所示，过y轴上一点M（0，2）的直线与抛物线交于A，B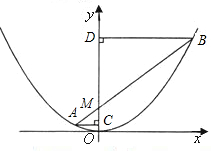两点，过点A，B分别作y轴的垂线，垂足分别为C，D．
（1）当点A的横坐标为-2时，求点B的坐标；
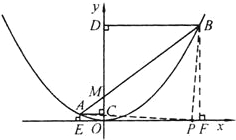
（2）在（1）的情况下，分别过点A，B作AE⊥x轴于E，BF⊥x轴于F，在EF上是否存在点P，使∠APB为直角？若存在，求点P的坐标；若不存在，请说明理由；
（3）当点A在抛物线上运动时（点A与点O不重合），求AC•BD的值．

Answer 1

解：（1）根据题意，设点B的坐标为（x，x²），其中x＞0．
∵点A的横坐标为-2，
∴A（-2，）．
∵AC⊥y轴，BD⊥y轴，M（0，2），
∴AC∥BD，MC=，MD=x²-2．
∴Rt△BDM∽Rt△ACM．
∴．
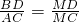即．
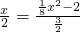解得x₁=-2（舍去），x₂=8．
∴B（8，8）．

（2）存在．
连接AP，BP，
由（1），AE=，BF=8，EF=10．
设EP=a，则PF=10-a．
∵AE⊥x轴，BF⊥x轴，∠APB=90°，
∴△AEP∽△PFB．
∴，
∴．
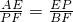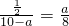解得a=5±．
经检验a=5±均为原方程的解，
∴点P的坐标为（3+，0）或（3-，0）．

（3）根据题意，设A（m，m²），B（n，n²），不妨设m＜0，n＞0．
由（1）知，
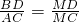则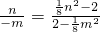或．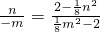
化简，得（mn+16）（m-n）=0．
∵m-n≠0，
∴mn=-16．
∴AC•BD=16．
分析：（1）已知二次函数解析式，及A点横坐标-2，可求A点纵坐标，故MC=2-=，设点B的坐标为（x，x²），由Rt△BDM∽Rt△ACM，得相似比，可求x的值，确定B点坐标；
（2）若∠APB=90°，利用互余关系可得出△AEP∽△PFB，设EP=a，则PF=10-a，而AE=，BF=8，利用相似比可求A，可得P的坐标；
（3）依题意设A（m，m²），B（n，n²），且m＜0，n＞0，由Rt△BDM∽Rt△ACM，类似（1），用含m，n的式子表示相关线段的长，利用相似比得出m，n的关系式，此时AC•BD=-mn．
点评：本题考查了点的坐标求法，相似三角形的判定及性质运用，要求掌握点的坐标与线段长的关系；
本题（1）也可以先求直线AM的解析式，再与抛物线解析式联立，求B点坐标．