题目内容
如图,矩形OABC的边OA,OC分别在x轴和y轴上,且点A的坐标为(4,0),点C 的坐标为(0,2),点P在线段CB上,距离
 轴3个单位,有一直
轴3个单位,有一直线y=kx+b(k≠0) 经过点P,且把矩形OABC分成两部分。

【小题1】若直线又经过
 轴上一点D,且把矩形OABC分成的两部分面积相等,
轴上一点D,且把矩形OABC分成的两部分面积相等,求k 和b的值
【小题2】若直线又经过矩形边上一点Q,且把矩形OABC分成的两部分的面积比
为3:29,求点Q坐标。
p;【答案】
【小题1】
【小题2】Q2(0, )解析:
)解析:
p;【解析】(1)设D(x,0),依题意得:
S矩=4×2=8,P(3,2)
S矩COAP= ×8=4
×8=4
S矩COAP= (x+3)×2=4
(x+3)×2=4
x=1
∴D(1,0)
 解得
解得
(2)S△PQ1B=

设Q1(4,y)
S△PQ1B= ×1×(2-y1)=
×1×(2-y1)=
y1=
∴Q1(4, )
)
设Q2(0,y2)
S△CQ2P= ×3×(2-y2)=
×3×(2-y2)=
y2=
∴Q2(0, )
)
【小题1】

【小题2】Q2(0,
 )解析:
)解析:p;【解析】(1)设D(x,0),依题意得:
S矩=4×2=8,P(3,2)
S矩COAP=
 ×8=4
×8=4 S矩COAP=
 (x+3)×2=4
(x+3)×2=4x=1
∴D(1,0)
 解得
解得
(2)S△PQ1B=


设Q1(4,y)
S△PQ1B=
 ×1×(2-y1)=
×1×(2-y1)=
y1=

∴Q1(4,
 )
) 设Q2(0,y2)
S△CQ2P=
 ×3×(2-y2)=
×3×(2-y2)=
y2=

∴Q2(0,
 )
) 
练习册系列答案
相关题目
 如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
如图,矩形OABC的顶点0、B的坐标分别是O(0,0)、B(8,4),顶点A在x轴上,顶点C在y轴上,把△OAB沿OB翻折,使点A落在点D的位置,BD与OA交于E.
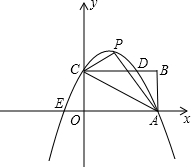 已知如图,矩形OABC的长OA=
已知如图,矩形OABC的长OA= (2013•樊城区模拟)已知如图,矩形OABC的长OA=2
(2013•樊城区模拟)已知如图,矩形OABC的长OA=2 如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是
如图,矩形OABC的顶点坐标分别是(0,0),(4,0),(4,1),(0,1),在矩形OABC的内部任取一点(x,y),则x<y的概率是