题目内容
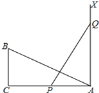
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点D是BC边的中点,
,点D是BC边的中点,![]() 于点E,
于点E,![]() 于点F.
于点F.

(1)![]() ________(用含α的式子表示)
________(用含α的式子表示)
(2)作射线DM与边AB交于点M,射线DM绕点D顺时针旋转![]() ,与AC边交于点N.根据条件补全图形,并写出DM与DN的数量关系,请说明理由.
,与AC边交于点N.根据条件补全图形,并写出DM与DN的数量关系,请说明理由.
【答案】(1)![]() ;(2)
;(2) ![]() ,理由见解析
,理由见解析
【解析】
(1)先利用等腰三角形的性质和三角形内角和得到∠B=∠C=90°-![]() ,然后利用互余可得到∠EDB=
,然后利用互余可得到∠EDB=![]() ;
;
(2)①如图,利用∠EDF=180°-2![]() 画图;
画图;
②先利用等腰三角形的性质得到DA平分∠BAC,再根据角平分线性质得到DE=DF,根据四边形内角和得到∠EDF=180°-2![]() ,所以∠MDE=∠NDF,然后证明△MDE≌△NDF得到DM=DN;
,所以∠MDE=∠NDF,然后证明△MDE≌△NDF得到DM=DN;
解:(1)∵AB=AC,
∴∠B=∠C=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ,
,
而DE⊥AB,
∴∠DEB=90°,
∴∠EDB=90°-∠B=90°-(90°-![]() )=
)=![]() ;
;
故答案为:![]() ;
;
(2)①补全图形如图所示.

②结论:![]() .
.
理由;在四边形AEDF中,![]() ,
,![]() 于点E,
于点E,![]() 于点F,
于点F,
∴![]() ,
,
连接AD,∵点D是BC边的中点,![]() ,
,
∴![]() ,
,
又∵射线DM绕点D顺时针旋转![]() 与AC边交于点N,
与AC边交于点N,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

【题目】个体户小王在上周日以每千克4元买进金佛山鲜笋![]() ,进入农贸市场后共占5个摊位,每个摊位最多容纳
,进入农贸市场后共占5个摊位,每个摊位最多容纳![]() 鲜笋,每个摊位的市场管理价为每天20元,下表为本周内鲜笋每天的销售价格与前一天相比价格的涨跌情况(涨记为正,跌记为负).星期一的价格是在周日每千克4元买进价格基础上涨了1.3元.
鲜笋,每个摊位的市场管理价为每天20元,下表为本周内鲜笋每天的销售价格与前一天相比价格的涨跌情况(涨记为正,跌记为负).星期一的价格是在周日每千克4元买进价格基础上涨了1.3元.
星期 | 一 | 二 | 三 | 四 | 五 |
与前一天相比价格的涨跌情况/元 | +1.3 | -0.1 | +0.25 | +0.2 | -0.5 |
当天的交易量/ | 2500 | 2000 | 3000 | 1500 | 1000 |
(1)鲜笋销售最高价格为每千克多少元?
(2)小王在上周日以每千克4元买进金佛山解笋![]() ,进入批发市场后共占5个摊位,小王在销售过程中采用逐步减少摊位个数的方法来降低成本,增加收益,这样他在本周的买卖中共赚了多少钱?请你帮他算一算?
,进入批发市场后共占5个摊位,小王在销售过程中采用逐步减少摊位个数的方法来降低成本,增加收益,这样他在本周的买卖中共赚了多少钱?请你帮他算一算?
【题目】王大伯计划在自家的鱼塘里投放普通鱼苗和红色鱼苗,需要购买这两种鱼苗2000尾,购买这两种鱼苗的相关信息如下表:
品种项目 | 单价(元/尾) | 养殖费用(元/尾) |
普通鱼苗 | 0.5 | 1 |
红色鱼苗 | 1 | 1 |
设购买普通鱼苗x尾,养殖这些鱼苗的总费用为y元.
(1)写出y(元)与x(尾)之间的函数关系式;
(2)如果购买每种鱼苗不少于600尾,在总鱼苗2000尾不变的条件下,养殖这些鱼苗的最低费用是多少?