题目内容
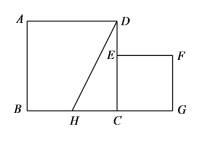
【题目】如图,已知正方形ABCD的边长为1,正方形CEFG的面积为![]() ,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为
,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为![]() ,且
,且![]() .
.
⑴求线段CE的长;
⑵若点H为BC边的中点,连结HD,求证:![]() .
.
【答案】(1)CE=![]() ;(2)见解析.
;(2)见解析.
【解析】
根据正方形的性质,
(1)先设CE=x(0<x<1),则DE=1-x,由S1=S2,列等式即可得到答案.
(2)根据勾股定理得到HD,再由H,C,G在同一直线上,得证HD=HG.
根据题意,得AD=BC=CD=1,∠BCD=90°.
(1)设CE=x(0<x<1),则DE=1-x,
因为S1=S2,所以x2=1-x,
解得x=![]() (负根舍去),
(负根舍去),
即CE=![]()
(2)因为点H为BC边的中点,
所以CH=![]() ,所以HD=
,所以HD=![]() ,
,
因为CG=CE=![]() ,点H,C,G在同一直线上,
,点H,C,G在同一直线上,
所以HG=HC+CG=![]() +
+![]() =
=![]() ,所以HD=HG
,所以HD=HG

练习册系列答案
相关题目