题目内容
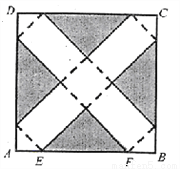
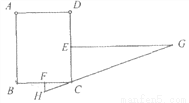
如图,在矩形ABCD中,E为AD边上的一点,过C点作CF⊥CE交AB的延长线于点F.
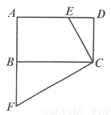
(1)求证:△CDE∽△CBF;
(2)若B为AF的中点,CB=3,DE=1,求CD的长.
(1)证明见解析;(2)CD= 【解析】试题分析:(1)如图,通过证明∠D=∠1,∠2=∠4即可得; (2)由△CDE∽△CBF,可得CD:CB=DE:BF,根据B为AF中点,可得CD=BF,再根据CB=3,DE=1即可求得. 试题解析:(1)∵四边形ABCD是矩形, ∴∠D=∠1=∠2+∠3=90° , ∵CF⊥CE, ∴∠4+∠3=90°, ∴∠2=∠...
练习册系列答案
相关题目
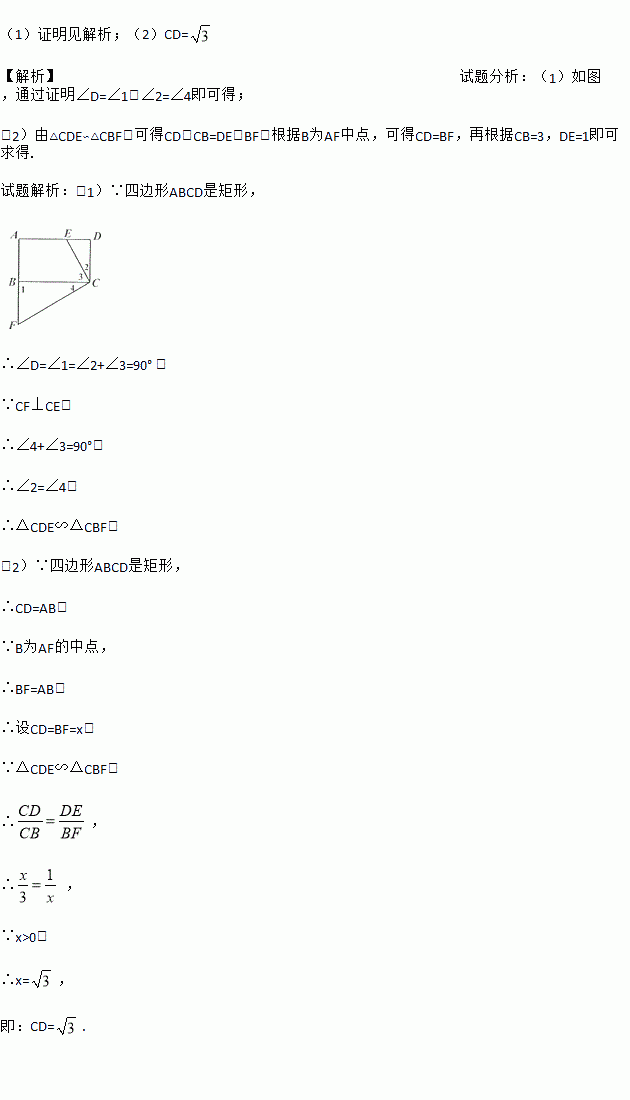

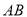 、
、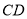 相交于
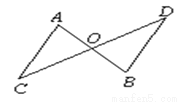
相交于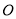 ,且OA=OB,观察图形:图中隐含一个相等的角,联想“
,且OA=OB,观察图形:图中隐含一个相等的角,联想“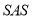 ”,只需补充条件 ,则有
”,只需补充条件 ,则有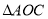 ≌
≌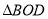 .
.
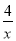 (x>0)的图象交于A(m,4),B(2,n)两点,与坐标轴分别交于M、N两点.
(x>0)的图象交于A(m,4),B(2,n)两点,与坐标轴分别交于M、N两点.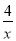 >0的解集;
>0的解集;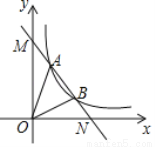
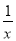 的图象上,则y1与y2的大小关系是( ).
的图象上,则y1与y2的大小关系是( ).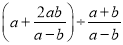 = .
= .