题目内容
11. 如图所示,BD、CE是△ABC的两条高,M是BC的中点,MN⊥ED于N,BC=10,DE=6,求MN的长.
如图所示,BD、CE是△ABC的两条高,M是BC的中点,MN⊥ED于N,BC=10,DE=6,求MN的长.
分析 连接DM,EM,根据直角三角形斜边上的中线等于斜边的一半可得EM=$\frac{1}{2}$BC,DM=$\frac{1}{2}$BC,从而得到EM=DM,再根据等腰三角形三线合一的性质和勾股定理解答.
解答 解:如图,
连接DM,EM,
∵M是BC的中点,BD、CE是△ABC的两条高,
∴EM=$\frac{1}{2}$BC=5,DM=$\frac{1}{2}$BC=5,
∴EM=DM,
∵N是DE的中点,
∴MN垂直平分DE,
∴EN=$\frac{1}{2}$DE=3,
∴MN=$\sqrt{E{M}^{2}-E{N}^{2}}$=4.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,勾股定理的运用,熟记性质并作辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1. 如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于E,若AC=10cm,则BD+DE=( )
如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于E,若AC=10cm,则BD+DE=( )
 如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于E,若AC=10cm,则BD+DE=( )
如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于E,若AC=10cm,则BD+DE=( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 9cm |
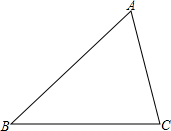 如图,△ABC,
如图,△ABC, 如图,已知△ABC中,AB=AC,取AC上一点D,使AD=BD.
如图,已知△ABC中,AB=AC,取AC上一点D,使AD=BD. 如图,已知∠DOE=90°,OD,OE分别是∠AOC与∠BOC的平分线,A,O,B三点在同一条直线上吗?为什么?
如图,已知∠DOE=90°,OD,OE分别是∠AOC与∠BOC的平分线,A,O,B三点在同一条直线上吗?为什么?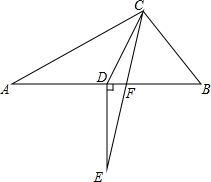 已知:在△ABC中,∠ACB=90°,CF是∠ACB的交平分线,点D在边AB上,∠ACD=∠A,ED⊥AB交CF的延长线于点E,求证:∠E=∠DCF.
已知:在△ABC中,∠ACB=90°,CF是∠ACB的交平分线,点D在边AB上,∠ACD=∠A,ED⊥AB交CF的延长线于点E,求证:∠E=∠DCF.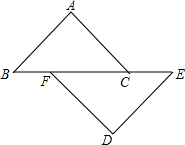 如图,在△ABC和△DEF中,点B、F、C,E在同一直线上,AB=DE,BF=EC,AB∥DE,求证:AC=DF.
如图,在△ABC和△DEF中,点B、F、C,E在同一直线上,AB=DE,BF=EC,AB∥DE,求证:AC=DF.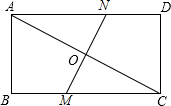 如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD折叠,使点C与点A重合,折痕交BC于M,交AC于O,交AD于N,求:
如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD折叠,使点C与点A重合,折痕交BC于M,交AC于O,交AD于N,求: