题目内容
阅读理解并
为了求1+2+22+23+24+…+22009的值，可令S=1+2+22+23+24+…+22009，
则2S=2+22+23+24+…+22009+22010，因此2S-S=（2+22+23+…+22009+22010）-（1+2+22+23+…+22009）=22010-1．
所以：S=22010-1．即1+2+22+23+24+…+22009=22010-1．
请依照此法，求：1+4+42+43+44+…+42010的值．
为了求1+2+22+23+24+…+22009的值，可令S=1+2+22+23+24+…+22009，
则2S=2+22+23+24+…+22009+22010，因此2S-S=（2+22+23+…+22009+22010）-（1+2+22+23+…+22009）=22010-1．
所以：S=22010-1．即1+2+22+23+24+…+22009=22010-1．
请依照此法，求：1+4+42+43+44+…+42010的值．
为了求1+4+42+43+44+…+42010的值，可令S=1+4+42+43+44+…+42010，
则4S=4+42+43+44+…+42011，
所以4S-S=（4+42+43+44+…+42011）-（1+4+42+43+44+…+42011）=42011-1，
所以3S=42011-1，
S=
（42011-1），
即1+4+42+43+44+…+42010=
（42011-1）．
则4S=4+42+43+44+…+42011，
所以4S-S=（4+42+43+44+…+42011）-（1+4+42+43+44+…+42011）=42011-1，
所以3S=42011-1，
S=
| 1 |
| 3 |
即1+4+42+43+44+…+42010=
| 1 |
| 3 |
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
的值，可令
，
， 因此
-
=
。
。即
的值。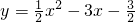
，且x的值在数1～4（包含1和4）之间变化，求这时y的变化范围．