题目内容
 如图,扇形AOB的圆心角为45°,半径长为
如图,扇形AOB的圆心角为45°,半径长为| 2 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
分析:由∠AOB为45°,得到△OAB为等腰直角三角形,于是OC=CB,而S阴影部分=S扇形OAB-S△OCB.然后根据扇形和等边三角形的面积公式计算即可.
解答:解:∵∠AOB为45°,BC⊥OA于点C,
∴△OCB为等腰直角三角形,OC=CB,
∵半径长为
,
∴OC2+BC2=OB2
S扇形OAB=
=
,
∴OC=BC=1,
∴S△OCB=
×1×1=
,
∴S阴影部分=S扇形OAB-S△OCB=
-
,
故答案为:
-
.
∴△OCB为等腰直角三角形,OC=CB,
∵半径长为
| 2 |
∴OC2+BC2=OB2
S扇形OAB=
45×π×(
| ||
| 360 |
| π |
| 4 |
∴OC=BC=1,
∴S△OCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴S阴影部分=S扇形OAB-S△OCB=
| π |
| 4 |
| 1 |
| 2 |
故答案为:
| π |
| 4 |
| 1 |
| 2 |
点评:本题考查了扇形面积的计算,是属于基础性的题目的一个组合,只要记住公式即可正确解出.关键是从图中可以看出阴影部分的面积是扇形的面积减去直角三角形的面积,

练习册系列答案
相关题目
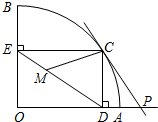 如图,扇形OAB的半径OA=r,圆心角∠AOB=90°,点C是
如图,扇形OAB的半径OA=r,圆心角∠AOB=90°,点C是
 (2012•珠海三模)如图:扇形OAB的圆心角∠AOB=120°,半径OA=6cm,
(2012•珠海三模)如图:扇形OAB的圆心角∠AOB=120°,半径OA=6cm, (1997•台湾)已知:如图,扇形AOB.求作:一个与OA、OB、
(1997•台湾)已知:如图,扇形AOB.求作:一个与OA、OB、 如图,扇形OAB的半径OA=r,圆心角∠AOB=90°,点C是
如图,扇形OAB的半径OA=r,圆心角∠AOB=90°,点C是 上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,点M在DE上,DM=2EM,过点C的直线CP交OA的延长线于点P,且∠CPO=∠CDE.
上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,点M在DE上,DM=2EM,过点C的直线CP交OA的延长线于点P,且∠CPO=∠CDE. r;
r;