题目内容
 如图,直线y=-2x-
如图,直线y=-2x-| 8 |
| 5 |
| k |
| x |
考点:反比例函数综合题
专题:
分析:首先证明DB=DA,再计算出A、B两点坐标,再根据勾股定理可得DA2=b2+(-
)2,再表示出DB2=[(b-(-
)]2,进而计算出b的值,从而算出AD的解析式,然后再计算出BC的解析式,再联立两个解析式,从而算出C点坐标,即可算出反比例函数的k值.
| 4 |
| 5 |
| 8 |
| 5 |
解答:解:设D(0,b),
在Rt△ABC中,
∵DC=BD,
∴∠DCB=∠DBC,
∵∠BAC+∠DCB=90°,∠DBC+∠DBA=90°,
∴∠DAB=∠DBA,
∴DB=DA,
在y=-2x-
中,当y=0,x=-
,当x=0,y=-
,
∴A(-
,0),B(0,-
),
∴DA2=b2+(-
)2,DB2=[(b-(-
)]2,
∴b2+(-
)2=[(b-(-
)]2,
解得:b=-
,
设AD解析式为y=mx+b,
-
m-
=0
解得:m=-
,
∴y=-
x-
,
∵BC⊥AB,AB的直线解析式为y=-2x-
,
∴BC的直线解析式为y=
x-
,
,
解得
,
∴C(
,-
),
∵双曲线y=
过点C点,
∴k=-
.
在Rt△ABC中,
∵DC=BD,
∴∠DCB=∠DBC,
∵∠BAC+∠DCB=90°,∠DBC+∠DBA=90°,
∴∠DAB=∠DBA,
∴DB=DA,
在y=-2x-
| 8 |
| 5 |
| 4 |
| 5 |
| 8 |
| 5 |
∴A(-
| 4 |
| 5 |
| 8 |
| 5 |
∴DA2=b2+(-
| 4 |
| 5 |
| 8 |
| 5 |
∴b2+(-
| 4 |
| 5 |
| 8 |
| 5 |
解得:b=-
| 3 |
| 5 |
设AD解析式为y=mx+b,
-
| 4 |
| 5 |
| 3 |
| 5 |
解得:m=-
| 3 |
| 4 |
∴y=-
| 3 |
| 4 |
| 3 |
| 5 |
∵BC⊥AB,AB的直线解析式为y=-2x-
| 8 |
| 5 |
∴BC的直线解析式为y=
| 1 |
| 2 |
| 8 |
| 5 |
|
解得
|
∴C(
| 4 |
| 5 |
| 6 |
| 5 |
∵双曲线y=
| k |
| x |
∴k=-
| 24 |
| 25 |
点评:此题主要考查了反比例函数综合,关键是根据关键条件DB=DC,计算出D点坐标,求出AD和BC的解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
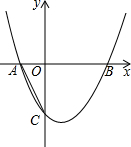 如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点,点A在x轴的负半轴,点B在x轴的正半轴,与y轴交于点C,且CO=2AO,CO=BO,AB=3.则下列判断中正确的是( )
如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点,点A在x轴的负半轴,点B在x轴的正半轴,与y轴交于点C,且CO=2AO,CO=BO,AB=3.则下列判断中正确的是( )| A、此抛物线的解析式为y=x2+x-2 | ||
| B、当x>0时,y随着x的增大而增大 | ||
C、此抛物线与直线y=-
| ||
| D、在此抛物线上的某点M,使△MAB的面积等于4,这样的点共有三个 |
如图,已知△ABC,则甲、乙、丙三个三角形中和△ABC全等的是( )


| A、只有乙 | B、甲和乙 |
| C、只有丙 | D、乙和丙 |