题目内容
已知AD是△ABC的中线,∠ABC=30°,∠ADC=45°,则∠ACB=分析:设AE=x,过A作AE⊥BC于E,根据三角形内角和定理求出∠DAE=45°,求出DE、BE、BD、DC、CE的长,根据锐角三角函数求出tan∠ACB即可.
解答: 解:设AE=x,
解:设AE=x,
过A作AE⊥BC,交BC延长线于E,
∵AE⊥BC,
∴∠AED=∠AEB=90°,
∵∠ADC=45°,
∴∠DAE=180°-90°-45°=45°=∠ADE,
∴AE=DE=x,
∵∠B=30°,
∴AB=2x,
由勾股定理得:BE=
x,
∴BD=DC=
x-x,
∴CE=x-(
x-x)=(2-
)x,
∵tan∠ACE=
=
=2+
,
∵tan75°=tan(45°+30°)=
=2+
∴∠ACE=75°,
则∠ACB=180°-75°=105°.
故答案为:105°.
 解:设AE=x,
解:设AE=x,过A作AE⊥BC,交BC延长线于E,
∵AE⊥BC,
∴∠AED=∠AEB=90°,
∵∠ADC=45°,
∴∠DAE=180°-90°-45°=45°=∠ADE,
∴AE=DE=x,
∵∠B=30°,
∴AB=2x,
由勾股定理得:BE=
| 3 |
∴BD=DC=
| 3 |
∴CE=x-(
| 3 |
| 3 |
∵tan∠ACE=
| AE |
| CE |
| x | ||
(2-
|
| 3 |
∵tan75°=tan(45°+30°)=
| tan45°-tan30° |
| 1-tan45°×tan30° |
| 3 |
∴∠ACE=75°,
则∠ACB=180°-75°=105°.
故答案为:105°.
点评:本题主要考查对解直角三角形,三角形的内角和定理,勾股定理,垂线,等腰三角形的性质和判定等知识点的理解和掌握,能用x表示出一些线段的长度是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
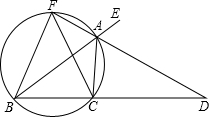 于点F,连接FB、FC.
于点F,连接FB、FC. 3、如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:①AG:AD=1:2;②GE:BE=1:4;③GE:BE=3:4,其中正确的为( )
3、如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:①AG:AD=1:2;②GE:BE=1:4;③GE:BE=3:4,其中正确的为( )
