题目内容
以直角坐标系原点为中心,将点A(-1,2)顺时针旋转90°后的坐标是________.
(2,1)
分析:根据题意画出A的对称点B,过A作AN⊥x轴于N,过B作BM⊥x轴于M,推出OA=OB,∠AOB=90°,∠ANO=∠BMO=90°,求出∠A=∠BOM,证△AON≌△OBM,推出AN=OM,ON=BM,根据A的坐标即可求出答案.
解答:如图: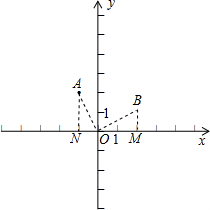
以直角坐标系原点为中心,将点A(-1,2)顺时针旋转90°后到B点,
过A作AN⊥x轴于N,过B作BM⊥x轴于M,
则OA=OB,∠AOB=90°,∠ANO=∠BMO=90°,
∴∠AON+∠BOM=180°-90°=90°,
∠A+∠AON=90°,
∴∠A=∠BOM
在△AON和△OBM中
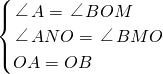 ,
,
∴△AON≌△OBM,
∴AN=OM,ON=BM,
∵A(-1,2),
∴OM=2,BM=1,
∴B(2,1).
故答案为:(2,1).
点评:本题考查了相似三角形的性质和判定,旋转的性质,坐标与图形性质,三角形的内角和定理等知识点的运用,关键是根据题意画出A的对称点B,主要培养了学生的画图能力和运用图形进行计算的能力,题型不错,难度也不大,是一道很具有代表性的题目.
分析:根据题意画出A的对称点B,过A作AN⊥x轴于N,过B作BM⊥x轴于M,推出OA=OB,∠AOB=90°,∠ANO=∠BMO=90°,求出∠A=∠BOM,证△AON≌△OBM,推出AN=OM,ON=BM,根据A的坐标即可求出答案.
解答:如图:
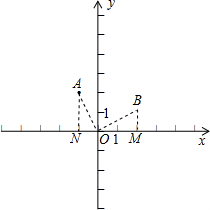
以直角坐标系原点为中心,将点A(-1,2)顺时针旋转90°后到B点,
过A作AN⊥x轴于N,过B作BM⊥x轴于M,
则OA=OB,∠AOB=90°,∠ANO=∠BMO=90°,
∴∠AON+∠BOM=180°-90°=90°,
∠A+∠AON=90°,
∴∠A=∠BOM
在△AON和△OBM中
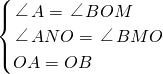 ,
,∴△AON≌△OBM,
∴AN=OM,ON=BM,
∵A(-1,2),
∴OM=2,BM=1,
∴B(2,1).
故答案为:(2,1).
点评:本题考查了相似三角形的性质和判定,旋转的性质,坐标与图形性质,三角形的内角和定理等知识点的运用,关键是根据题意画出A的对称点B,主要培养了学生的画图能力和运用图形进行计算的能力,题型不错,难度也不大,是一道很具有代表性的题目.

练习册系列答案
相关题目
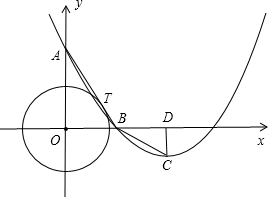 A(0,4)作⊙O的切线交x轴于点B,T是切点,抛物线y=ax2+bx+c的顶点为C(3,-
A(0,4)作⊙O的切线交x轴于点B,T是切点,抛物线y=ax2+bx+c的顶点为C(3,-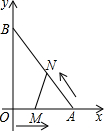 (2012•湛江)如图,在平面直角坐标系中,直角三角形AOB的顶点A、B分别落在坐标轴上.O为原点,点A的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒
(2012•湛江)如图,在平面直角坐标系中,直角三角形AOB的顶点A、B分别落在坐标轴上.O为原点,点A的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒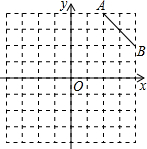 如图,已知A(2,4),B(4,2),C是第一象限内的一个格点(小正方形的顶点,叫格点),由点C与线段AB组成一个以AB为底,腰长为无理数的等腰三角形.
如图,已知A(2,4),B(4,2),C是第一象限内的一个格点(小正方形的顶点,叫格点),由点C与线段AB组成一个以AB为底,腰长为无理数的等腰三角形.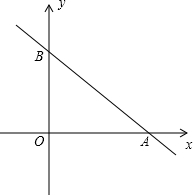 点到达A点时终止运动.
点到达A点时终止运动. 如图,以直角坐标系的原点O为圆心作⊙O,点M、N是⊙O上的两点,M(-1,2),N(2,1)
如图,以直角坐标系的原点O为圆心作⊙O,点M、N是⊙O上的两点,M(-1,2),N(2,1)