题目内容
在平面直角坐标系xOy中,直线AB与x轴交于点A(8,0),与y轴交于点B(0,6).动点P自原点O向A点运动,速度为1个单位/秒;动点Q自原点O沿折线O-B-A运动,速度为2个单位/秒;P、Q两点同时运动,设运动时间为t秒,P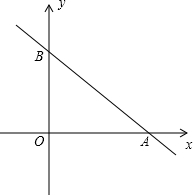 点到达A点时终止运动.
点到达A点时终止运动.
(1)当Q点在线段BA上运动时,请直接用t表示Q点的坐标.
(2)当t>3时,求tan∠QPO的值.
(3)在整个运动过程中是否存在这样的t值,使得△OQP是直角三角形?如果存在,请求出t的取值范围或相应的t值;如果不存在,请说明理由.
(4)当t为何值时,△OPQ是以OQ为腰的等腰三角形?请直接写出此时的t值.
 点到达A点时终止运动.
点到达A点时终止运动.(1)当Q点在线段BA上运动时,请直接用t表示Q点的坐标.
(2)当t>3时,求tan∠QPO的值.
(3)在整个运动过程中是否存在这样的t值,使得△OQP是直角三角形?如果存在,请求出t的取值范围或相应的t值;如果不存在,请说明理由.
(4)当t为何值时,△OPQ是以OQ为腰的等腰三角形?请直接写出此时的t值.
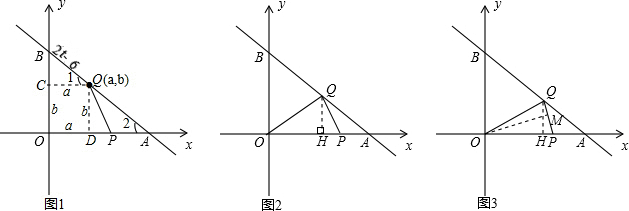
分析:(1)如图1,设Q(a,b),利用直角三角函数的定义来求点Q的坐标.
(2)如图1,当t>3时,点Q在线段AB上.在Rt△PQD中,利用∠QDO的正切函数的定义来解答即可;
(3)需要分类讨论:①当点Q在OB边上运动时,△OQP总是直角三角形;②当点Q在边BA上运动时,如图1,只有∠OQP=90°,然后利用(2)中的正切函数值来求t的取值;
(4)需要分类讨论:①当OQ=OP时,以求得t值;②当OQ=OP时,如图3,来求t的值.
(2)如图1,当t>3时,点Q在线段AB上.在Rt△PQD中,利用∠QDO的正切函数的定义来解答即可;
(3)需要分类讨论:①当点Q在OB边上运动时,△OQP总是直角三角形;②当点Q在边BA上运动时,如图1,只有∠OQP=90°,然后利用(2)中的正切函数值来求t的取值;
(4)需要分类讨论:①当OQ=OP时,以求得t值;②当OQ=OP时,如图3,来求t的值.
解答:解:(1)如图1,点Q在线段AB上,设Q(a,b).过点Q作QC⊥OB于点C,过点Q作QD⊥OA于点D.
∵点A(8,0),点B(0,6).
∴OB=6,OA=8.
∴在Rt△AOB中,根据勾股定理求得AB=10.
∵CQ∥OA,
∴∠1=∠2,
∴cos∠1=cos∠2,即
=
,
∴
=
,
解得,a=
.
又∵sin∠2=
=
,即
=
,
解得b=
,
∴Q点坐标为(
,
);
(2)如图1,当t>3时,点Q在线段AB上.
由(1)知,OD=a=
∴PD=OP-OD=t-a=
,
又由(1)知,QD=b=
,
∴tan∠QPO=
=
=2,即tan∠QPO=2;
(3)当点Q在OB边上运动时,△OQP总是直角三角形,此时0<t≤3;
当点Q在边BA上运动时,如图1,只有∠OQP=90°,过Q点作QH⊥OA,垂足为H,
则tan∠QPO=tan∠OQH=
=2,
∴
:
=2,
解得t=6.
∴当0<t≤3或t=6时,△OQP是直角三角形;
(4)当OQ=PQ时,易求t=
;
当OQ=OP时,如图3,过O点作OM⊥PQ,垂足为M;过Q点作QH⊥OP,垂足为H.
设HP=x,则QH=2x,QP=
x,QM=PM=
x,OM=
x,OP=
x,OH=
x,
∴OH:OP=3:5,
:t=3:5解得t=4.8.
当t=
或4.8时,△OPQ是以OQ为腰的等腰三角形.
∵点A(8,0),点B(0,6).
∴OB=6,OA=8.
∴在Rt△AOB中,根据勾股定理求得AB=10.
∵CQ∥OA,
∴∠1=∠2,
∴cos∠1=cos∠2,即
| OA |
| AB |
| CQ |
| BQ |
∴
| 8 |
| 10 |
| a |
| 2t-6 |
解得,a=
| 8t-24 |
| 5 |
又∵sin∠2=
| OB |
| AB |
| b |
| 10-(2t-6) |
| 6 |
| 10 |
| b |
| 16-2t |
解得b=
| 48-6t |
| 5 |
∴Q点坐标为(
| 8t-24 |
| 5 |
| 48-6t |
| 5 |
(2)如图1,当t>3时,点Q在线段AB上.
由(1)知,OD=a=
| 8t-24 |
| 5 |
∴PD=OP-OD=t-a=
| 24-3t |
| 5 |
又由(1)知,QD=b=
| 48-6t |
| 5 |
∴tan∠QPO=
| QD |
| PD |
| ||
|
(3)当点Q在OB边上运动时,△OQP总是直角三角形,此时0<t≤3;
当点Q在边BA上运动时,如图1,只有∠OQP=90°,过Q点作QH⊥OA,垂足为H,
则tan∠QPO=tan∠OQH=
| OH |
| QH |
∴
| 8t-24 |
| 5 |
| 48-6t |
| 5 |
解得t=6.
∴当0<t≤3或t=6时,△OQP是直角三角形;
(4)当OQ=PQ时,易求t=
| 48 |
| 11 |
当OQ=OP时,如图3,过O点作OM⊥PQ,垂足为M;过Q点作QH⊥OP,垂足为H.
设HP=x,则QH=2x,QP=
| 5 |
| ||
| 2 |
| 5 |
| 5 |
| 2 |
| 3 |
| 2 |
∴OH:OP=3:5,
| 8t-24 |
| 5 |
当t=
| 48 |
| 11 |

点评:本题考查了一次函数综合题.注意“数形结合”与“分类讨论”的数学思想在本题解答过程中的应用.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点. 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为