题目内容
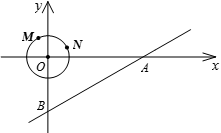
 如图,以直角坐标系的原点O为圆心作⊙O,点M、N是⊙O上的两点,M(-1,2),N(2,1)
如图,以直角坐标系的原点O为圆心作⊙O,点M、N是⊙O上的两点,M(-1,2),N(2,1)(1)试在x轴上找点P使PM+PN最小,求出P点的坐标;
(2)若在坐标系中另有一直线AB,A(10,0),点B在y轴上,∠BAO=30°,⊙O以0.2个单位/秒的速度沿x轴正方向运动,问圆在运动过程中与该直线相交的时间有多长?
分析:(1)作点N关于X轴的对称点Q,连结M、Q交x轴于点P,则P就是使PM+PN最小的点,根据关于x轴对称的点的坐标特点求出Q点的坐标,用待定系数法求出直线MQ的解析式,求出当y=0时x的值即可得出P点坐标;
(2)M(-1,2)在圆O上,所以根据勾股定理可求出⊙O的半径,再根据OA=10,∠BAO=30°可得出原点O到直线AB的距离为5,当圆运动到圆心到直线AB的距离等于半径时圆与直线AB相切,此时可求出圆心O可在点A左侧或右侧与A的距离,再由⊙O以0.2个单位/秒的速度沿x轴正方向运动即可得出结论.
(2)M(-1,2)在圆O上,所以根据勾股定理可求出⊙O的半径,再根据OA=10,∠BAO=30°可得出原点O到直线AB的距离为5,当圆运动到圆心到直线AB的距离等于半径时圆与直线AB相切,此时可求出圆心O可在点A左侧或右侧与A的距离,再由⊙O以0.2个单位/秒的速度沿x轴正方向运动即可得出结论.
解答: 解:(1)如图1所示,作点N关于x轴的对称点Q,连结M、Q交x轴于点P,则P就是使PM+PN最小的点,
解:(1)如图1所示,作点N关于x轴的对称点Q,连结M、Q交x轴于点P,则P就是使PM+PN最小的点,
∵N(2,1),
∴Q(2,-1),
设直线MQ的解析式为y=kx+b(k≠0),
∵M(-1,2),Q(2,-1),
∴
,
解得
,
∴直线MQ的解析式为:y=-x+1,
∵当y=0时,x=1,
∴P点坐标为(1,0);

(2)∵M(-1,2)在圆O上,
∴圆O的半径=
=
,
∵OA=10,∠BAO=30°,
∴原点O到直线AB的距离为5,
∴当圆运动到圆心到直线AB的距离OD=
时圆与直线AB相切当⊙O在直线AB的左侧时,如图2所示:
∵∠BAO=30°,
∴OA=2
,
同理,当⊙O在直线AB的左侧时,圆心与点A的距离也等于2
,
∵⊙O以0.2个单位/秒的速度沿x轴正方向运动,
∴相交时间=
=20
(秒).
答:圆在运动过程中与该直线相交的时间有20
秒.
 解:(1)如图1所示,作点N关于x轴的对称点Q,连结M、Q交x轴于点P,则P就是使PM+PN最小的点,
解:(1)如图1所示,作点N关于x轴的对称点Q,连结M、Q交x轴于点P,则P就是使PM+PN最小的点,∵N(2,1),
∴Q(2,-1),
设直线MQ的解析式为y=kx+b(k≠0),
∵M(-1,2),Q(2,-1),
∴
|
解得
|
∴直线MQ的解析式为:y=-x+1,
∵当y=0时,x=1,
∴P点坐标为(1,0);

(2)∵M(-1,2)在圆O上,
∴圆O的半径=
| 22+12 |
| 5 |
∵OA=10,∠BAO=30°,
∴原点O到直线AB的距离为5,
∴当圆运动到圆心到直线AB的距离OD=
| 5 |
∵∠BAO=30°,
∴OA=2
| 5 |
同理,当⊙O在直线AB的左侧时,圆心与点A的距离也等于2
| 5 |
∵⊙O以0.2个单位/秒的速度沿x轴正方向运动,
∴相交时间=
2
| ||||
| 0.2 |
| 5 |
答:圆在运动过程中与该直线相交的时间有20
| 5 |
点评:本题考查的是圆的综合题,熟知圆与直线的位置关系及用待定系数法求一次函数的解析式等知识是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目