Question

如图1，点P是△ABD中AD边上一点，当P为AD中点时，则有S_△ABP=

1

2

S_△BDP，如图2，在四边形ABCD中，P是AD边上任意一点，探究：
（1）当AP=

1

2

AD时，如图3，△PBC与△ABC和△DBC的面积之间有什么关系？写出求解过程；
（2）当AP=

1

3

AD时，探究S_△PBC与S_△ABC和S_△DBC之间的关系，写出求解过程；
（3）一般地，当AP=

1

n

AD（n表示正整数）时，探究S_△PBC与S_△ABC和S_△DBC之间的关系，写出求解过程；
（4）当AP=

m

n

AD（0≤

m

n

≤1）时，直接写出S_△PBC与S_△ABC和S_△DBC之间的关系．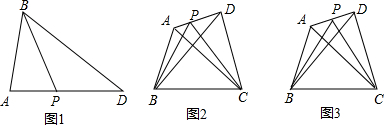

Answer 1

分析：（1）根据AP=

1

2

AD，△ABP和△ABD的高相等，得出△CDP和△CDA的高相等，进而得出S_△PBC=S_{四边形ABCD}-S_△ABP-S_△CDP，整理求出即可；
（2）仿照（1）的方法，只需把

1

2

换为

1

3

；
（3）注意由（1）（2）得到一定的规律；得到面积和线段比值之间的一般关系；
（4）利用（3），得到更普遍的规律．

解答：解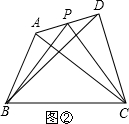：（1）当AP=

1

2

AD时（如图②）：
∵AP=

1

2

AD，△ABP和△ABD的高相等，
∴S_△ABP=

1

2

S_△ABD．
∵PD=AD-AP=

1

2

AD，△CDP和△CDA的高相等，
∴S_△CDP=

1

2

S_△CDA．
∴S_△PBC=S_{四边形ABCD}-S_△ABP-S_△CDP
=S_{四边形ABCD}-

1

2

S_△ABD-

1

2

S_△CDA
=S_{四边形ABCD}-

1

2

（S_{四边形ABCD}-S_△DBC）-

1

2

（S_{四边形ABCD}-S_△ABC）
=

1

2

S_△DBC+

1

2

S_△ABC．

（2）∵AP=

1

3

AD，△ABP和△ABD的高相等，
∴S_△ABP=

1

3

S_△ABD．
又∵PD=AD-AP=

2

3

AD，△CDP和△CDA的高相等，
∴S_△CDP=

2

3

S_△CDA．
∴S_△PBC=S_{四边形ABCD}-S_△ABP-S_△CDP
=S_{四边形ABCD}-

1

3

S_△ABD-

2

3

S_△CDA
=S_{四边形ABCD}-

1

3

（S_{四边形ABCD}-S_△DBC）-

2

3

（S_{四边形ABCD}-S_△ABC）
=

1

3

S_△DBC+

2

3

S_△ABC．
∴S_△PBC=

1

3

S_△DBC+

2

3

S_△ABC

（3）S_△PBC=

1

n

S_△DBC+

n-1

n

S_△ABC；
∵AP=

1

n

AD，△ABP和△ABD的高相等，
∴S_△ABP=

1

n

S_△ABD．
又∵PD=AD-AP=

n-1

n

AD，△CDP和△CDA的高相等，
∴S_△CDP=

n-1

n

S_△CDA
∴S_△PBC=S_{四边形ABCD}-S_△ABP-S_△CDP
=S_{四边形ABCD}-

1

n

S_△ABD-

n-1

n

S_△CDA
=S_{四边形ABCD}-

1

n

（S_{四边形ABCD}-S_△DBC）-

n-1

n

（S_{四边形ABCD}-S_△ABC）
=

1

n

S_△DBC+

n-1

n

S_△ABC．
∴S_△PBC=

1

n

S_△DBC+

n-1

n

S_△ABC

（4）S_△PBC=

m

n

S_△DBC+

n-m

n

S_△ABC．

点评：此题主要考查了面积以及等积变换，注意总结相应规律，类似问题通常采用类比的方法求解是解题关键．