题目内容
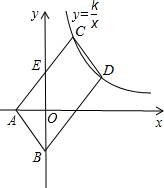
如图，C为双曲线y=
（x＞0）上一点，线段AE与y轴交于点E，且AE=EC，将线段AC平移至BD处，点D恰好也在双曲线y=
（x＞0）上，若A（-1，0），B（0，-2）．则k=______．
| k |
| x |
| k |
| x |
过点C作CN⊥y轴于点N，CM⊥x轴于点M，DQ⊥y轴于点Q，DF⊥x轴于点F，
在△NCE与△OAE中，
∵
，
∴△NCE≌△OAE，
∴AO=NC=1，
则设C点坐标为：（1，y），
∵A（-1，0），B（0，-2），又因为线段AC平移至BD处，
∴D点坐标为：（2，y-2），
∵C，D都在反比例函数图象上，
∴1×y=k，2（y-2）=k，
∴y=2（y-2），
解得：y=4，
∴C点坐标为：（1，4），
∴k=1×4=4．
故答案为：4．
在△NCE与△OAE中，
∵
|
∴△NCE≌△OAE，
∴AO=NC=1，
则设C点坐标为：（1，y），
∵A（-1，0），B（0，-2），又因为线段AC平移至BD处，
∴D点坐标为：（2，y-2），
∵C，D都在反比例函数图象上，
∴1×y=k，2（y-2）=k，
∴y=2（y-2），
解得：y=4，
∴C点坐标为：（1，4），
∴k=1×4=4．
故答案为：4．
练习册系列答案
相关题目
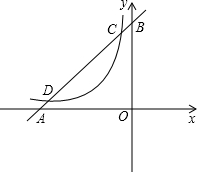D，且点C的坐标为（-1，2）
