ЬтФПФкШн
ЁОЬтФПЁПЃЈЮЪЬтГЪЯжЃЉАЂЛљУзЕТелЯвЖЈРэЃК
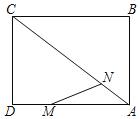
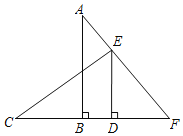
ШчЭМ1ЃЌABКЭBCЪЧЁбOЕФСНЬѕЯвЃЈМДелЯпABCЪЧдВЕФвЛЬѕелЯвЃЉЃЌBCЃОABЃЌЕуMЪЧ![]() ЕФжаЕуЃЌдђДгMЯђBCЫљзїДЙЯпЕФДЙзуDЪЧелЯвABCЕФжаЕуЃЌМДCDЃНDB+BAЃЎЯТУцЪЧдЫгУЁАНиГЄЗЈЁБжЄУїCDЃНDB+BAЕФВПЗжжЄУїЙ§ГЬЃЎ
ЕФжаЕуЃЌдђДгMЯђBCЫљзїДЙЯпЕФДЙзуDЪЧелЯвABCЕФжаЕуЃЌМДCDЃНDB+BAЃЎЯТУцЪЧдЫгУЁАНиГЄЗЈЁБжЄУїCDЃНDB+BAЕФВПЗжжЄУїЙ§ГЬЃЎ
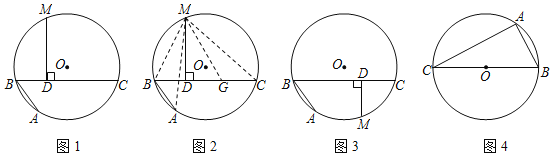
жЄУїЃКШчЭМ2ЃЌдкCDЩЯНиШЁCGЃНABЃЌСЌНгMAЁЂMBЁЂMCКЭMGЃЎ
ЁпMЪЧ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ
ЁрMAЃНMCЂй
гжЁпЁЯAЃНЁЯCЂк
ЁрЁїMABЁеЁїMCGЂл
ЁрMBЃНMG
гжЁпMDЁЭBC
ЁрBDЃНDG
ЁрAB+BDЃНCG+DG
МДCDЃНDB+BA
ИљОнжЄУїЙ§ГЬЃЌЗжБ№аДГіЯТСаВНжшЕФРэгЩЃК
ЂйЁЁ ЁЁЃЌ
ЂкЁЁ ЁЁЃЌ
ЂлЁЁ ЁЁЃЛ
ЃЈРэНтдЫгУЃЉШчЭМ1ЃЌABЁЂBCЪЧЁбOЕФСНЬѕЯвЃЌABЃН4ЃЌBCЃН6ЃЌЕуMЪЧ![]() ЕФжаЕуЃЌMDЁЭBCгкЕуDЃЌдђBDЃНЁЁ ЁЁЃЛ
ЕФжаЕуЃЌMDЁЭBCгкЕуDЃЌдђBDЃНЁЁ ЁЁЃЛ
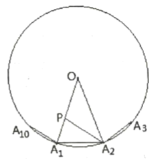
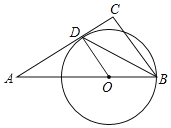
ЃЈБфЪНЬНОПЃЉШчЭМ3ЃЌШєЕуMЪЧ![]() ЕФжаЕуЃЌЃЈЮЪЬтГЪЯжЃЉжаЕФЦфЫћЬѕМўВЛБфЃЌХаЖЯCDЁЂDBЁЂBAжЎМфДцдкдѕбљЕФЪ§СПЙиЯЕЃПВЂМгвджЄУїЃЎ
ЕФжаЕуЃЌЃЈЮЪЬтГЪЯжЃЉжаЕФЦфЫћЬѕМўВЛБфЃЌХаЖЯCDЁЂDBЁЂBAжЎМфДцдкдѕбљЕФЪ§СПЙиЯЕЃПВЂМгвджЄУїЃЎ
ЃЈЪЕМљгІгУЃЉИљОнФуЖдАЂЛљУзЕТелЯвЖЈРэЕФРэНтЭъГЩЯТСаЮЪЬтЃК
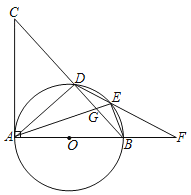
ШчЭМ4ЃЌBCЪЧЁбOЕФжБОЖЃЌЕуAдВЩЯвЛЖЈЕуЃЌЕуDдВЩЯвЛЖЏЕуЃЌЧвТњзуЁЯDACЃН45ЁуЃЌШєABЃН6ЃЌЁбOЕФАыОЖЮЊ5ЃЌЧѓADГЄЃЎ
ЁОД№АИЁПЃЈЮЪЬтГЪЯжЃЉЯрЕШЕФЛЁЫљЖдЕФЯвЯрЕШЃЛЭЌЛЁЫљЖдЕФдВжмНЧЯрЕШЃЛгаСНзщБпМАЦфМаНЧЗжБ№ЖдгІЯрЕШЕФСНИіШ§НЧаЮШЋЕШЃЛЃЈРэНтдЫгУЃЉ1ЃЛЃЈБфЪНЬНОПЃЉDBЃНCD+BAЃЛжЄУїМћНтЮіЃЛЃЈЪЕМљгІгУЃЉ7![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈЮЪЬтГЪЯжЃЉИљОндВЕФаджЪМДПЩЧѓНтЃЛ
ЃЈРэНтдЫгУЃЉCDЃНDB+BAЃЌМДCDЃН6ЉCD+ABЃЌМДCDЃН6ЉCD+4ЃЌНтЕУЃКCDЃН5ЃЌМДПЩЧѓНтЃЛ
ЃЈБфЪНЬНОПЃЉжЄУїЁїMABЁеЁїMGBЃЈSASЃЉЃЌдђMAЃНMGЃЌMCЃНMGЃЌгжDMЁЭBCЃЌдђDCЃНDGЃЌМДПЩЧѓНтЃЛ
ЃЈЪЕМљгІгУЃЉвбжЊЁЯD1ACЃН45ЁуЃЌЙ§ЕуD1зїD1G1ЁЭACгкЕуG1ЃЌдђCG1Ёф+ABЃНAG1ЃЌЫљвдAG1ЃН![]() ЃЈ6+8ЃЉЃН7ЃЎШчЭМЁЯD2ACЃН45ЁуЃЌЭЌРэвзЕУAD2ЃН
ЃЈ6+8ЃЉЃН7ЃЎШчЭМЁЯD2ACЃН45ЁуЃЌЭЌРэвзЕУAD2ЃН![]() ЃЎ
ЃЎ
ЃЈЮЪЬтГЪЯжЃЉ
ЂйЯрЕШЕФЛЁЫљЖдЕФЯвЯрЕШ
ЂкЭЌЛЁЫљЖдЕФдВжмНЧЯрЕШ
ЂлгаСНзщБпМАЦфМаНЧЗжБ№ЖдгІЯрЕШЕФСНИіШ§НЧаЮШЋЕШ
ЙЪД№АИЮЊЃКЯрЕШЕФЛЁЫљЖдЕФЯвЯрЕШЃЛЭЌЛЁЫљЖЈвхЕФдВжмНЧЯрЕШЃЛгаСНзщБпМАЦфМаНЧЗжБ№ЖдгІЯрЕШЕФСНИіШ§НЧаЮШЋЕШЃЛ
ЃЈРэНтдЫгУЃЉCDЃНDB+BAЃЌМДCDЃН6ЉCD+ABЃЌМДCDЃН6ЉCD+4ЃЌНтЕУЃКCDЃН5ЃЌ
BDЃНBCЉCDЃН6Љ5ЃН1ЃЌ
ЙЪД№АИЮЊЃК1ЃЛ
ЃЈБфЪНЬНОПЃЉDBЃНCD+BAЃЎ
жЄУїЃКдкDBЩЯНиШЅBGЃНBAЃЌСЌНгMAЁЂMBЁЂMCЁЂMGЃЌ
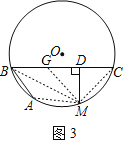
ЁпMЪЧЛЁACЕФжаЕуЃЌ
ЁрAMЃНMCЃЌЁЯMBAЃНЁЯMBGЃЎ
гжMBЃНMB
ЁрЁїMABЁеЁїMGBЃЈSASЃЉ
ЁрMAЃНMG
ЁрMCЃНMGЃЌ
гжDMЁЭBCЃЌ
ЁрDCЃНDGЃЌ
AB+DCЃНBG+DGЃЌ
МДDBЃНCD+BAЃЛ
ЃЈЪЕМљгІгУЃЉ
ШчЭМЃЌBCЪЧдВЕФжБОЖЃЌЫљвдЁЯBACЃН90ЁуЃЎ
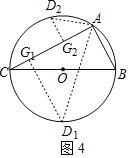
вђЮЊABЃН6ЃЌдВЕФАыОЖЮЊ5ЃЌЫљвдACЃН8ЃЎ
вбжЊЁЯD1ACЃН45ЁуЃЌЙ§ЕуD1зїD1G1ЁЭACгкЕуG1ЃЌ
дђCG1Ёф+ABЃНAG1ЃЌ
ЫљвдAG1ЃН![]() ЃЈ6+8ЃЉЃН7ЃЎ
ЃЈ6+8ЃЉЃН7ЃЎ
ЫљвдAD1ЃН7![]() ЃЎ
ЃЎ
ШчЭМЁЯD2ACЃН45ЁуЃЌЭЌРэвзЕУAD2ЃН![]() ЃЎ
ЃЎ
ЫљвдADЕФГЄЮЊ7![]() Лђ
Лђ![]() ЃЎ
ЃЎ