题目内容
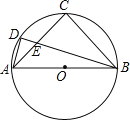
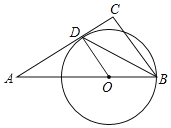
【题目】如图,在△ABC中,O是AB边上的点,以O为圆心,OB为半径的⊙0与AC相切于点D,BD平分∠ABC,AD=![]() OD,AB=12,求CD的长.
OD,AB=12,求CD的长.
【答案】CD=2![]() .
.
【解析】
由切线的性质得出AC⊥OD,求出∠A=30°,证出∠ODB=∠CBD,得出OD∥BC,得出∠C=∠ADO=90°,由直角三角形的性质得出∠ABC=60°,BC=![]() AB=6,得出∠CBD=30°,再由直角三角形的性质即可得出结果.
AB=6,得出∠CBD=30°,再由直角三角形的性质即可得出结果.
∵⊙O与AC相切于点D,
∴AC⊥OD,
∴∠ADO=90°,
∵AD=![]() OD,
OD,
∴tanA=![]() =
=![]() ,
,
∴∠A=30°,
∵BD平分∠ABC,
∴∠OBD=∠CBD,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODB=∠CBD,
∴OD∥BC,
∴∠C=∠ADO=90°,
∴∠ABC=60°,
∴BC=![]() AB=6,
AB=6,
∴∠CBD=![]() ∠ABC=30°,
∠ABC=30°,
∴CD=![]() BC=
BC=![]() ×6=2
×6=2![]() .
.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
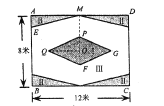
【题目】如图,某校准备给长12米,宽8米的矩形![]() 室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形
室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形![]() ),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点
),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点![]() 为矩形和菱形的对称中心,
为矩形和菱形的对称中心,![]() ,
,![]() ,
,![]() ,为了美观,要求区域Ⅱ的面积不超过矩形
,为了美观,要求区域Ⅱ的面积不超过矩形![]() 面积的
面积的![]() ,若设
,若设![]() 米.
米.
甲 | 乙 | 丙 | |
单价(元/米2) |
|
|
|
(1)当![]() 时,求区域Ⅱ的面积.
时,求区域Ⅱ的面积.
(2)计划在区域Ⅰ,Ⅱ分别铺设甲,乙两款不同的深色瓷砖,区域Ⅲ铺设丙款白色瓷砖,
①在相同光照条件下,当场地内白色区域的面积越大,室内光线亮度越好.当![]() 为多少时,室内光线亮度最好,并求此时白色区域的面积.
为多少时,室内光线亮度最好,并求此时白色区域的面积.
②三种瓷砖的单价列表如下,![]() 均为正整数,若当
均为正整数,若当![]() 米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时
米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时![]() __________,
__________,