题目内容
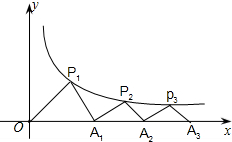 如图,P1(x1,y1),P2(x2,y2),在函数y=
如图,P1(x1,y1),P2(x2,y2),在函数y=| 4 | x |
分析:过点P1作P1B⊥x轴,垂足为B,△P1OA1是等腰直角三角形,所以X1=Y1.P1(x1,y1)在函数y=
(x>0)的图象上,X1=Y2=2,即P1B=OB=2,△P1OA1是等腰直角三角形,推出OA1=4.
过点P2作P2C⊥x轴,垂足为C,△P2A1A2,△P3A2A3都是等腰直角三角形,所以A1C=P2C=Y2,OC=OA1+A1C=4+Y2=X2,P2(x2,y2),在函数y=
(x>0)的图象上,所以y2=
,解得y2=2
-2,x2=2+2
,则P2的坐标是(2
+2,2
-2).
| 4 |
| x |
过点P2作P2C⊥x轴,垂足为C,△P2A1A2,△P3A2A3都是等腰直角三角形,所以A1C=P2C=Y2,OC=OA1+A1C=4+Y2=X2,P2(x2,y2),在函数y=
| 4 |
| x |
| 4 |
| x2 |
| 2 |
| 2 |
| 2 |
| 2 |
解答: 解:过点P1作P1B⊥x轴,垂足为B,△P1OA1是等腰直角三角形,
解:过点P1作P1B⊥x轴,垂足为B,△P1OA1是等腰直角三角形,
∴x1=y1.
∵P1(x1,y1)在函数y=
(x>0)的图象上,x1=y2=2,即P1B=OB=2,
∴△P1OA1是等腰直角三角形,
∴OA1=4.
过点P2作P2C⊥x轴,垂足为C,△P2A1A2,△P3A2A3都是等腰直角三角形,
∴A1C=P2C=y2,OC=OA1+A1C=4+y2=x2,
∵P2(x2,y2)在函数y=
(x>0)的图象上,
∴y2=
,解得:y2=2
-2,x2=2+2
,
∴P2的坐标是(2
+2,2
-2).
 解:过点P1作P1B⊥x轴,垂足为B,△P1OA1是等腰直角三角形,
解:过点P1作P1B⊥x轴,垂足为B,△P1OA1是等腰直角三角形,∴x1=y1.
∵P1(x1,y1)在函数y=
| 4 |
| x |
∴△P1OA1是等腰直角三角形,
∴OA1=4.
过点P2作P2C⊥x轴,垂足为C,△P2A1A2,△P3A2A3都是等腰直角三角形,
∴A1C=P2C=y2,OC=OA1+A1C=4+y2=x2,
∵P2(x2,y2)在函数y=
| 4 |
| x |
∴y2=
| 4 |
| x2 |
| 2 |
| 2 |
∴P2的坐标是(2
| 2 |
| 2 |
点评:考查反比例函数性质与等腰直角三角形的性质等知识.巧妙借助反比例函数图象性质与等腰直角三角形的性质相结合,综合性很强.

练习册系列答案
相关题目
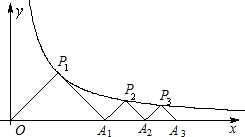 图象上,△P1OA1,△P2A1A2,△P3A2A3,…△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…An-1An都在x轴上
图象上,△P1OA1,△P2A1A2,△P3A2A3,…△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…An-1An都在x轴上
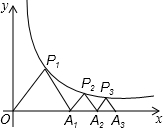 如图,P1(x1,y1),P2(x2,y2),Pn(xn,yn),…在函数
如图,P1(x1,y1),P2(x2,y2),Pn(xn,yn),…在函数  如图,P1(x1,y1),P2(x2,y2),…Pn(xn,yn)在函数
如图,P1(x1,y1),P2(x2,y2),…Pn(xn,yn)在函数