题目内容
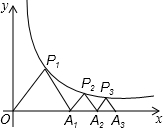 如图,P1(x1,y1),P2(x2,y2),Pn(xn,yn),…在函数 y=
如图,P1(x1,y1),P2(x2,y2),Pn(xn,yn),…在函数 y=2
| ||
| x |
分析:由已知,△P1OA1,△P2A1A2,△P3A2A3,△PnAn-1An都是等边三角形,边OA1、A1A2、A2A3,…An-1An都在x轴上,所以得:
∠P1OA1=60°,即得OP1所在的直线为y=tan60°x,也就是说点P1在直线OP1上,又P1(x1,y1)在函数 y=
(x>0)的图象上,所以得:y1=tan60°x1,y1=
,由此求出x1,y1,即点P1的坐标.
∠P1OA1=60°,即得OP1所在的直线为y=tan60°x,也就是说点P1在直线OP1上,又P1(x1,y1)在函数 y=
2
| ||
| x |
2
| ||
| x1 |
解答:解:已知△P1OA1是等边三角形,
∴∠P1OA160°,
又OA1在x轴上,
∴OP1所在的直线为y=tan60°x,且点P1(x1,y1)在直线OP1上,
∴得:y1=tan60°x1 ①
又点P1(x1,y1)在函数 y=
(x>0)的图象上,
∴得:y1=
②
由已知x>0,所以由①②解得:
x1=
,y1=
,
即点P1的坐标为:(
,
),
故答案为:(
,
).
∴∠P1OA160°,
又OA1在x轴上,
∴OP1所在的直线为y=tan60°x,且点P1(x1,y1)在直线OP1上,
∴得:y1=tan60°x1 ①
又点P1(x1,y1)在函数 y=
2
| ||
| x |
∴得:y1=
2
| ||
| x1 |
由已知x>0,所以由①②解得:
x1=
| 2 |
| 6 |
即点P1的坐标为:(
| 2 |
| 6 |
故答案为:(
| 2 |
| 6 |
点评:此题考查的知识点是反比例函数应用,解答此题的关键是由已知等边三角形得到OP1所在的直线,即点P1(x1,y1)在直线上,又在函数 y=
(x>0)的图象上,所以得到x1和y1的方程组,从而求出x1和y1.
2
| ||
| x |

练习册系列答案
相关题目
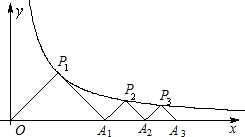 图象上,△P1OA1,△P2A1A2,△P3A2A3,…△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…An-1An都在x轴上
图象上,△P1OA1,△P2A1A2,△P3A2A3,…△PnAn-1An都是等腰直角三角形,斜边OA1、A1A2、A2A3,…An-1An都在x轴上
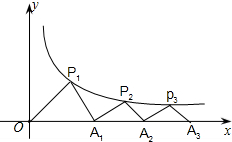 如图,P1(x1,y1),P2(x2,y2),在函数y=
如图,P1(x1,y1),P2(x2,y2),在函数y= 如图,P1(x1,y1),P2(x2,y2),…Pn(xn,yn)在函数
如图,P1(x1,y1),P2(x2,y2),…Pn(xn,yn)在函数