题目内容
4.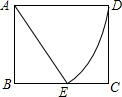 如图,矩形ABCD中,AD=4,AB=2$\sqrt{3}$,以点A为圆心,AD为半径画弧交BC于点E,所得的扇形的弧长为$\frac{4π}{3}$.
如图,矩形ABCD中,AD=4,AB=2$\sqrt{3}$,以点A为圆心,AD为半径画弧交BC于点E,所得的扇形的弧长为$\frac{4π}{3}$.
分析 根据余弦的定义求出∠BAE的度数,根据矩形的性质求出∠DAE的度数,根据弧长的公式l=$\frac{nπr}{180}$计算即可.
解答 解:由题意得,AE=AD=4,
cos∠BAE=$\frac{AB}{AE}$=$\frac{2\sqrt{3}}{4}$=$\frac{\sqrt{3}}{2}$,
则∠BAE=30°,
∴∠DAE=60°,
扇形的弧长=$\frac{60π×4}{180}$=$\frac{4π}{3}$,
故答案为:$\frac{4π}{3}$.
点评 本题考查的是扇形的弧长的计算,掌握弧长的公式:l=$\frac{nπr}{180}$是解题的关键.

练习册系列答案
相关题目
14.下列调查中,适合采用普查的是( )
| A. | 调查全国中学生心理健康现状 | |
| B. | 调查我市食品合格情况 | |
| C. | 调查你所在的班级同学的身高情况 | |
| D. | 调查桂林电视台某电视节目的收视率 |
15.某同学一周中每天体育运动所花时间(单位:分钟)分别为:35,40,45,40,55,40,48,这组数据的中位数是( )
| A. | 35 | B. | 40 | C. | 45 | D. | 55 |
12.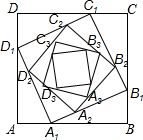 如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )
如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )
 如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )
如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )| A. | $\frac{8}{9}{a}^{2}$ | B. | ($\frac{4}{9}$)na2 | C. | ($\frac{5}{9}$)n-1a2 | D. | ($\frac{5}{9}$)na2 |
9. 如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )
如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )
 如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )
如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )| A. | 40° | B. | 50° | C. | 60° | D. | 30° |
16.我们知道,中式窗户的图案非常多样,美轮美奂,在下面几个比较简单的窗户图案中,可以看作是轴对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.一组数据6,x,8,10,16的平均数为10,则这组数据的众数、中位数分别是( )
| A. | 10,16 | B. | 8,10 | C. | 10,12 | D. | 10,10 |
 如图,AB是⊙O的直径,C是⊙O外一点,过点E作⊙O的两条切线ED,EB,切点分别为点D,B.连接AD并延长交BE延长线于点C,连接OE.
如图,AB是⊙O的直径,C是⊙O外一点,过点E作⊙O的两条切线ED,EB,切点分别为点D,B.连接AD并延长交BE延长线于点C,连接OE.