题目内容
 如图所示,直线AB与x交于A(1,0),与y轴交于B(0,-3),若直线AB上的点C在第三象限,且S△BOC=2,求点C的坐标.
如图所示,直线AB与x交于A(1,0),与y轴交于B(0,-3),若直线AB上的点C在第三象限,且S△BOC=2,求点C的坐标.考点:一次函数图象上点的坐标特征
专题:
分析:先用待定系数法求出直线AB的解析式,再设出C点坐标,利用三角形的面积公式求解即可.
解答:解:设直线AB的解析式为y=kx+b(k≠0),
∵A(1,0),B(0,-3),
∴
,解得
,
∴直线AB的解析式为;y=3x-3,
∵点C在直线AB上,且在第三象限,
∴设C(x,3x-3).
∵S△BOC=2,
∴S△BOC=
OB•|x|=
×3×(-x)=2,
∴x=-
.
∴3x-3=3×(-
)-3=-7.
∴C(-
,-7).
∵A(1,0),B(0,-3),
∴
|
|
∴直线AB的解析式为;y=3x-3,
∵点C在直线AB上,且在第三象限,
∴设C(x,3x-3).
∵S△BOC=2,
∴S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴x=-
| 4 |
| 3 |
∴3x-3=3×(-
| 4 |
| 3 |
∴C(-
| 4 |
| 3 |
点评:本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
满足方程y3=x2+x的整数解有( )组.
| A、1 | B、2 | C、3 | D、4 |
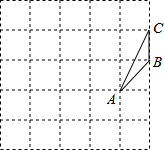 如图,由边长为1的25个小正方形组成的正方形网络上有一个三角形ABC;在网络上画一个与三角形ABC相似的且面积最大的三角形,使它的三个顶点都落在小正方形的顶点上,并请你算一算,这个三角形的最大面积是多少?
如图,由边长为1的25个小正方形组成的正方形网络上有一个三角形ABC;在网络上画一个与三角形ABC相似的且面积最大的三角形,使它的三个顶点都落在小正方形的顶点上,并请你算一算,这个三角形的最大面积是多少?