题目内容
n个正整数a1,a2,…,an满足如下条件:1=a1<a2<…<an=2009;且a1,a2,…,an中任意n-1个不同的数的算术平均数都是正整数.求n的最大值.
【答案】分析:设a1,a2,an中去掉ai后剩下的n-1个数的算术平均数为正整数bi,从而可推出n-1能整除(aj-ai),然后根据an-1=(an-an-1)+(an-1-an-2)+…+(a2-a1)≥(n-1)+(n-1)+…+(n-1)=(n-1)2,可得出n的范围,从而结合题意可得出n的值.
解答:解:设a1,a2,an中去掉ai后剩下的n-1个数的算术平均数为正整数bi,i=1,2,n.即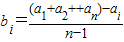 .
.
于是,对于任意的1≤i<j≤n,都有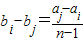 ,
,
从而n-1|(aj-ai),
由于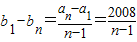 是正整数,
是正整数,
故n-1|23×251,
由于an-1=(an-an-1)+(an-1-an-2)+…+(a2-a1)≥(n-1)+(n-1)+…+(n-1)=(n-1)2,
所以,(n-1)2≤2008,于是n≤45,
结合n-1|23×251,所以,n≤9;
另一方面,令a1=8×0+1,a2=8×1+1,a3=8×2+1,a8=8×7+1,
a9=8×251+1,则这9个数满足题设要求.
综上所述,n的最大值为9.
点评:本题考查数的整除性问题,难度较大,在解答时要抓住a1,a2,…,an中任意n-1个不同的数的算术平均数都是正整数这个条件进行解答.
解答:解:设a1,a2,an中去掉ai后剩下的n-1个数的算术平均数为正整数bi,i=1,2,n.即
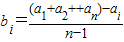 .
.于是,对于任意的1≤i<j≤n,都有
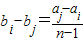 ,
,从而n-1|(aj-ai),
由于
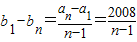 是正整数,
是正整数,故n-1|23×251,
由于an-1=(an-an-1)+(an-1-an-2)+…+(a2-a1)≥(n-1)+(n-1)+…+(n-1)=(n-1)2,
所以,(n-1)2≤2008,于是n≤45,
结合n-1|23×251,所以,n≤9;
另一方面,令a1=8×0+1,a2=8×1+1,a3=8×2+1,a8=8×7+1,
a9=8×251+1,则这9个数满足题设要求.
综上所述,n的最大值为9.
点评:本题考查数的整除性问题,难度较大,在解答时要抓住a1,a2,…,an中任意n-1个不同的数的算术平均数都是正整数这个条件进行解答.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目