题目内容
图1所示的遮阳伞,伞柄垂直于水平地面,其示意图如图2.当伞收紧时,点P与点A重合;当伞慢慢撑开时,动点P由A向B移动;当点P到达点B时,伞张得最开.已知伞在撑开的过程中,总有PM=PN=CM=CN=6.0分米,CE=CF=18.0分米,BC=2.0分米.
(1)求AP长的取值范围;
(2)当∠CPN=60°时,求AP的值;
(3)在阳光垂直照射下,伞张得最开时,求伞下的阴影(假定为圆面)面积S(结果保留π).

(1)求AP长的取值范围;
(2)当∠CPN=60°时,求AP的值;
(3)在阳光垂直照射下,伞张得最开时,求伞下的阴影(假定为圆面)面积S(结果保留π).

考点:相似三角形的应用
专题:
分析:(1)根据题意,得AC=CN+PN,进一步求得AB的长,即可求得AP的取值范围;
(2)根据等边△PCN的判定和性质即可求解;
(3)连接MN、EF,分别交AC于B、H.此题根据菱形CMPN的性质求得MB的长,再根据相似三角形的对应边的比相等,求得圆的半径,再利用二次函数增减性求出即可.
(2)根据等边△PCN的判定和性质即可求解;
(3)连接MN、EF,分别交AC于B、H.此题根据菱形CMPN的性质求得MB的长,再根据相似三角形的对应边的比相等,求得圆的半径,再利用二次函数增减性求出即可.
解答:解:(1)∵BC=2.0分米,AC=CN+PN=12分米,
∴AB=12-2=10(分米),
∴AP的取值范围为:0分米≤AP≤10分米.
(2)∵CN=PN,∠CPN=60°,
∴△PCN等边三角形.
∴CP=6分米.
∴AP=AC-PC=12-6=6(分米),
即当∠CPN=60°时,AP=6分米;
(2)连接MN、EF,分别交AC于B、H.
设AP=x分米,
∵PM=PN=CM=CN,
∴四边形PNCM是菱形.
∴MN与PC互相垂直平分,AC是∠ECF的平分线,
PB=
.
在Rt△MBP中,PM=6分米,
∴MB2=PM2-PB2=62-(6-
x)2=6x-
x2.
∵CE=CF,AC是∠ECF的平分线,
∴EH=HF,EF⊥AC.
∵∠ECH=∠MCB,∠EHC=∠MBC=90°,
∴△CMB∽△CEH.
∴
=
.
∴
=(
)2=
,
∴EH2=9•MB2=9•(6x-
x2).
∴S=π•EH2=9π(6x-
x2),
即S=-
πx2+54πx,
∵x=-
=12,0≤x≤10,
∴x=10时,S最大=-
π×100+54π×10=315π(平方分米).
∴AB=12-2=10(分米),
∴AP的取值范围为:0分米≤AP≤10分米.
(2)∵CN=PN,∠CPN=60°,
∴△PCN等边三角形.
∴CP=6分米.
∴AP=AC-PC=12-6=6(分米),
即当∠CPN=60°时,AP=6分米;
(2)连接MN、EF,分别交AC于B、H.
设AP=x分米,
∵PM=PN=CM=CN,
∴四边形PNCM是菱形.
∴MN与PC互相垂直平分,AC是∠ECF的平分线,
PB=
| PC |
| 2 |
在Rt△MBP中,PM=6分米,
∴MB2=PM2-PB2=62-(6-
| 1 |
| 2 |
| 1 |
| 4 |
∵CE=CF,AC是∠ECF的平分线,
∴EH=HF,EF⊥AC.

∵∠ECH=∠MCB,∠EHC=∠MBC=90°,
∴△CMB∽△CEH.
∴
| MB |
| EH |
| CM |
| CE |
∴
| MB2 |
| EH2 |
| 6 |
| 18 |
| 1 |
| 9 |
∴EH2=9•MB2=9•(6x-
| 1 |
| 4 |
∴S=π•EH2=9π(6x-
| 1 |
| 4 |
即S=-
| 9 |
| 4 |
∵x=-
| b |
| 2a |
∴x=10时,S最大=-
| 9 |
| 4 |
点评:此题主要考查了相似三角形的应用以及菱形的性质和二次函数的应用,熟练运用菱形的性质、相似三角形的性质得出S与x的函数关系式是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列图形中,能折叠成正方体的是( )
A、 |
B、 |
C、 |
D、 |
 已知:如图∠A=∠F,∠C=∠D,∠1=70°,则∠2=( )度.
已知:如图∠A=∠F,∠C=∠D,∠1=70°,则∠2=( )度.| A、120 | B、90 |
| C、70 | D、110 |
下列四个图标中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
下列统计量中,不能反映一名学生在九年级第一学期的数学成绩稳定程度的是( )
| A、方差 | B、平均数 |
| C、标准差 | D、极差 |
分式方程
=
的解是( )
| 2 |
| x-3 |
| 12 |
| x2-9 |
| A、3 | B、-3 | C、±3 | D、无解 |
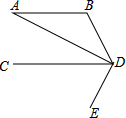 如图,已知AB∥CD,DA平分∠BDC,∠ADE=90°,∠B=120°,求∠BDE的度数.
如图,已知AB∥CD,DA平分∠BDC,∠ADE=90°,∠B=120°,求∠BDE的度数.